Wstęp
W ostatnim czasie mamy do czynienia z zalewem informacji pochodzących z różnych źródeł, a co się z tym wiąże - powstaje problem ich szybkiego i efektywnego przetwarzania oraz selekcji. Wielkie bazy danych będące coraz częściej niezbędnym elementem procesu zarządzania, olbrzymie zasoby wiedzy korporacyjnej, różne formy sieciowej działalności gospodarczej (e-business), Internet jako źródło wiedzy wykorzystywanej przez miliony ludzi. To tylko niektóre wybrane elementy obrazujące rozmiar i znaczenie tego zjawiska.
Tradycyjne techniki przetwarzania informacji nie zawsze dają oczekiwany efekt w rozsądnym czasie. Ponadto w szybko zmieniających się warunkach działania wielu przedsiębiorstw i związanych z nimi systemów informatycznych, pojawia się konieczność szybkiego dostosowywania istniejących algorytmów do nowych warunków, a to nie jest rzeczą ani łatwą, ani tanią.
Często także nie istnieją ani teoretyczne ani praktyczne rozwiązania dla przedstawionych powyżej problemów. Tymczasem rozwiązanie przynajmniej niektórych problemów może być znalezione, pod warunkiem, że w obszar rozwiązań dopuszczalnych włączone zostaną metody niestandardowe (jak chociażby sieci neuronowe), co na pewno przyniesie korzyść dla gospodarki, techniki i indywidualnych podmiotów, które uzyskać mogą przewagę konkurencyjną.
Sieci neuronowe od czasu swych narodzin w latach czterdziestych przeżywały okresy wzlotów i upadków. Od początkowej fascynacji ich możliwościami, poprzez znaczny spadek zainteresowania, wręcz zapomnienia po książce Minskiego[1], aż po renesans w latach osiemdziesiątych i dziewięćdziesiątych.
Inspiracją dla tej dziedziny nauki, modelem, do którego, początkowo bezpośrednio, odwoływali się badacze sieci neuronowych jest mózg. Ten najbardziej skomplikowany i tajemniczy z ludzkich organów stanowi dla nas ciągle zagadkę. Dzisiejsze, tak szerokie i powszechne zainteresowanie sieciami neuronowymi zarówno wśród inżynierów, przedstawicieli nauk ścisłych - matematyki i fizyki oraz biologów czy neurofizjologów wynika przede wszystkim z poszukiwań nad sposobami budowy bardziej efektywnych i bardziej niezawodnych urządzeń do przetwarzania informacji, a układ nerwowy jest tutaj niedościgłym wzorem. Z punktu widzenia dzisiejszej informatyki ważne jest nie tyle całościowe modelowanie mózgu, ile możliwość wykorzystania sposobów, jakimi on przetwarza informacje. Ciekawy z punktu widzenia informatyki jest także fakt, że dzięki tym modelom można rozwiązywać zadania, z którymi z trudem radzą sobie inne techniki obliczeniowe. Sieci neuronowe bowiem, mogą być stosowane wszędzie tam, gdzie pojawiają się problemy związane z przetwarzaniem i analizą danych, z ich predykcją, klasyfikacją czy sterowaniem. Można pokusić się nawet o stwierdzenie, że łatwiej wymienić problemy, w których sieci neuronowe się nie sprawdzą, od tych w których z powodzeniem można je zastosować (i w których zapewne były już stosowane). Głównym czynnikiem przemawiającym za praktycznym stosowaniem sieci neuronowych jest ich zdolność do uogólnień zdobytej wiedzy, która daje im jak gdyby pewną dozę inteligencji. Ciekawym i równie ważnym czynnikiem jest to, że sieci neuronowe są wyposażone w swoje wewnętrzne algorytmy przetwarzania informacji, które umożliwiają im rozwiązywanie nawet gatunkowo różnych zadań. Sposób w jaki sieć neuronowa zyskuje wiedzę o zadanym problemie, polega na nauce na podstawie znanych poprawnych przykładach (zwanych wzorcami uczącymi) rozwiązania danego problemu, lub prościej na bazie obserwacji prezentowanej jej wiedzy. Celem nauki jest sposób opisania wewnętrznych korelacji zachodzących pomiędzy wzorcami uczącymi. Na tej podstawie nauczona sieć neuronowa potrafi odpowiadać na pytania zarówno z zakresu wzorców uczących jak i spoza nich.
Mózg człowieka ciągle jest najpotężniejszym z istniejących obecnie urządzeń liczących do celów przetwarzania informacji w czasie rzeczywistym. Fascynacje mózgiem, jego własnościami (odpornością na uszkodzenia, równoległym przetwarzaniem itp.) już w latach 40-tych zaowocowały pracami, których fundamentalne znaczenie odczuwamy jeszcze dzisiaj.
Choć niewielu z nas potrafi przemnożyć w pamięci dwie liczby dwucyfrowe, co bez problemu robi najprostszy kalkulator, każdy bezbłędnie rozpoznaje twarze znajomych osób, z czym komputery mają jeszcze olbrzymie problemy. Mózg może pokonać nawet najszybszy superkomputer, pomimo że w tym procesie neurony jako jednostki przetwarzające są o wiele rzędów wielkości wolniejsze od swoich elektronicznych czy optoelektronicznych odpowiedników.
Sieci neuronowe odziedziczyły po swoim pierwowzorze kilka cech odróżniających ich działanie od innych systemów przetwarzania danych, a upodabniających je do mózgu. I choć nie mają monopolu na naśladowanie mózgu, to właśnie najczęściej sieci neuronowe odczytują ręczne pismo, prognozują kursy akcji na giełdzie, rozpoznają mowę, obrazy czy twarze.
Budowa i zasada funkcjonowania sztucznych sieci neuronowych
Mówiąc o sieciach neuronowych w aspekcie technicznym w istocie mamy na myśli sztuczne sieci neuronowe będące niezwykle okrojonym modelem rzeczywistości, gdyż jak wynika z badań anatomicznych na ludzki mózg składa się około 10 miliardów komórek nerwowych - neuronów, a sztuczna sieć (modelowana sieć) neuronowa w przeważającej większości posiada nie więcej niż kilkaset takich elementarnych "komórek" - sztucznych neuronów. Schematycznie sztuczny neuron przedstawia rys 1.
Rys. 1. Model sztucznego neuronu
Sztuczny neuron można zdefiniować w następujący sposób:
- Do neuronu docierają pewne sygnały, czyli wartości wejściowe. Są to albo wartości pierwotne pochodzące z zewnątrz i służące do zadawania danych dla obliczeń wykonywanych przez sieć, albo są to sygnały już częściowo przetworzone i pochodzące z wyjść innych neuronów. Należy przy tym zauważyć, że każdy neuron posiada zależną od potrzeb liczbęn wejść i dokładnie jedno wyjście. Wejścia na rysunku oznaczone są jakou1 doup natomiast wyjście jakoy
- Wartości docierające do neuronu są przemnażane przez pewien współczynnik liczbowy zwany wagą synaptyczną (wi), która zazwyczaj dla każdego wejścia przyjmuje inną wartość, ustalaną w procesie uczenia
- Wyznaczenie zagregowanej wartości wejściowej w bloku sumacyjnym, będącej ważoną sumą wejść
- Zagregowana wartość wejściowa reprezentująca łączne pobudzenie neuronu przekształcana jest zazwyczaj przez ustaloną funkcję aktywacji neuronu (zwaną inaczej funkcją przejścia). W charakterze funkcji aktywacji może być zastosowanych wiele różnych funkcji matematycznych, jednak ze względu na tematykę artykułu omówienie ich nie jest konieczne
Możliwości pojedynczego neuronu w zakresie przetwarzania informacji są stosunkowo niewielkie i z tego względu najczęściej stosowane są (podobnie jak w przypadku układów nerwowych organizmów żywych) połączone ze sobą grupy sztucznych neuronów (czyli sieci neuronowe), pozwalające na przeprowadzanie znacznie bardziej złożonych obliczeń.
Rys. 2. Struktura przykładowej sztucznej sieci neuronowej
Neurony wchodzące w skład sztucznej sieci neuronowej ułożone są najczęściej w warstwach. Wartości wyjściowe wyznaczone dla neuronów jednej warstwy wprowadzane są na wejścia neuronów warstwy następnej. Wyjątkiem jest tu warstwa pierwsza (zwanawarstwą wejściową) składająca się z neuronów, do których wejść doprowadzane są wartości zmiennych obserwowanych na zewnątrz sieci oraz warstwa ostatnia (wyjściowa), składająca się z neuronów wyznaczających wynik obliczeń traktowany jako wartość wyjściową całej sieci. Warstwy znajdujące się pomiędzy warstwą wejściową i wyjściową nazywane sąwarstwami ukrytymi, które wypracowują pewne dane pośrednie, będące podstawą dla procesu wyznaczania ostatecznego rozwiązania.
Sieć neuronowa w trakcie swojego działania przetwarza wprowadzone na jej wejścia wartości zmiennych wejściowych w wyniku czego uzyskiwane są na jej wyjściach wartości zmiennych wyjściowych. Sposób pracy sieci uzależniony jest od wielu czynników, do których należy zaliczyć przede wszystkim:
- Przyjęte modele neuronów - a więc wybrane dla neuronów sieci konkretne postacie funkcji agregującej i funkcji aktywacji; zwykle wszystkie neurony wchodzące w skład tej samej warstwy korzystają z takich samych formuł funkcji agregującej i funkcji aktywacji, natomiast w różnych warstwach stosowane są często neurony korzystające z różniących się formuł;
- Typ sieci neuronowej - Sieć uczona w trybie z nauczycielem (np. MLP, RBF), lub uczona w trybie bez nauczyciela (np. sieć Kohonena);
- Wartości współczynników wagowych neuronów - są one ustalane automatycznie w trakcie procesu uczenia i dlatego są różne dla poszczególnych wejść i dla poszczególnych neuronów;
- Liczba warstw sieci;
- Liczba neuronów w poszczególnych warstwach sieci;
- Przyjęty sposób połączeń neuronów.
Warunkiem koniecznym do właściwego funkcjonowania sieci jest poprawne określenie wszystkich wymienionych powyżej czynników.
Zanim zostaną pokazane możliwości prognostyczne sieci neuronowych na przykładzie Giełdy Papierów Wartościowych, co na pewno szczególnie interesuje czytelnika, parę słów na temat sposobów uczenia sieci neuronowych.
Uczenie sieci neuronowych
Pewne podobieństwa pomiędzy rzeczywistymi i sztucznymi sieciami neuronowymi można dostrzec nie tylko w ich budowie, ale również w sposobie pozyskiwania wiedzy niezbędnej do ich prawidłowego funkcjonowania. Proces pozyskiwania wiedzy przez sieć neuronową musi gwarantować możliwość późniejszego jej uogólniania w celu rozwiązania całego postawionego przed nią zadania (a nie tylko odtworzenia wiedzy zgromadzonej w tzw. zbiorze uczącym).
Proces przygotowania sieci do prawidłowego działania nazywany jest uczeniem. Sieć uczy się prawidłowo działać na podstawie prezentowanych jej przykładów. Bazując na przedstawionych rzeczywistych przypadkach sieć stara się odkryć i zapamiętać ogólne prawidłowości charakteryzujące te obiekty. Rozpoznane reguły sztuczna sieć neuronowa przechowuje w postaci rozproszonej w wartościach współczynników wagowych neuronów. Proces uczenia polega zatem na prawidłowym określeniu wartości współczynników wagowych neuronów na podstawie informacji wydobytych w trakcie procesu uczenia ze zbioru uczącego.
Kluczowym elementem w procesie uczenia są wagi wejść poszczególnych neuronów. Jeśli zmienią się wartości wag - neuron zacznie pełnić innego rodzaju funkcję w sieci, a co za tym idzie cała sieć zacznie inaczej działać. Uczenie sieci polega więc na tym, by tak dobrać wagi, aby wszystkie neurony wykonywały dokładnie takie czynności, jakich się od nich wymaga.
Uczenie sieci rozpoczyna się od nadania wagom neuronów wartości losowych. W każdym kroku iteracyjnego procesu uczenia wartości wag jednego lub kilku neuronów ulegają zmianie, przy czym reguły tych zmian są tak pomyślane, by każdy neuron sam potrafił określić, które ze swoich wag ma zmienić, w którą stronę, a także o ile. Możliwe są dwa warianty procesu uczenia:
- z nauczycielem
- bez nauczyciela
Uczenie z nauczycielem polega na tym, że sieci podaje się przykłady poprawnego działania, które powinna ona potem naśladować w swoim bieżącym działaniu (w czasie egzaminu). Przykład należy rozumieć w ten sposób, że nauczyciel podaje konkretne sygnały wejściowe i wyjściowe, pokazując jaka jest wymagana odpowiedź sieci dla pewnej konfiguracji danych wejściowych. Mamy do czynienia z parą wartości - przykładowym sygnałem wejściowym i pożądanym (oczekiwanym) wyjściem, czyli wymaganą odpowiedzią sieci na ten sygnał wejściowy. Zbiór przykładów zgromadzonych w celu ich wykorzystania w procesie uczenia sieci nazywa się zwykle ciągiem uczącym. Zatem w typowym procesie uczenia sieć otrzymuje od nauczyciela ciąg uczący i na jego podstawie uczy się prawidłowego działania, stosując jedną z wielu znanych dziś strategii uczenia.
U podstaw większości algorytmów uczenia z nauczycielem leży reguła Delta wprowadzona przez Widrowa i Hoffa. Polega ona na tym, że każdy neuron po otrzymaniu na swoich wejściach określonych sygnałów, wyznacza swój sygnał wyjściowy, wykorzystując posiadaną wiedzę w postaci wcześniej ustalonych wartości współczynników wagowych wszystkich wejść oraz progu. Wartość sygnału wyjściowego, wyznaczonego przez neuron na danym kroku procesu uczenia, porównywana jest z odpowiedzią wzorcową podaną przez nauczyciela w ciągu uczącym. Jeśli występuje rozbieżność - neuron wyznacza różnicę pomiędzy swoim sygnałem wyjściowym a tą wartością sygnału, która byłaby - według nauczyciela - prawidłowa. Ta różnica oznaczana jest zwykle symbolem greckiej litery ? (delta) i stąd nazwa opisywanej metody.
Sygnał błędu (delta) wykorzystywany jest przez neuron do korygowania swoich współczynników wagowych, stosując następujące reguły:
- wagi zmieniane są tym silniej, im większy błąd został wykryty
- wagi związane z tymi wejściami, na których występowały duże wartości sygnałów wejściowych, zmieniane są bardziej, niż wagi wejść, na których sygnał wejściowy był niewielki
Znając zatem błąd popełniony przez neuron oraz jego sygnały wejściowe możemy łatwo przewidzieć, jak będą się zmieniać jego wagi.
Obok opisanego wyżej schematu uczenia z nauczycielem występuje też szereg metod tak zwanego uczenia bez nauczyciela (albo samouczenia sieci). Samouczenie jest też bardzo interesujące z punktu widzenia zastosowań, gdyż nie wymaga żadnej jawnie podawanej do sieci neuronowej zewnętrznej wiedzy, a sieć zgromadzi wszystkie potrzebne informacje i wiadomości. Jest to jedna z najpopularniejszych metod samouczenia sieci neuronowych. Uczenie bez nauczyciela polega na tym, że sieci pokazuje się kolejne przykłady sygnałów wejściowych, nie podając żadnych informacji o tym, co z tymi sygnałami należy zrobić. Sieć obserwuje otoczenie i odbiera różne sygnały. Nikt nie określa jednak, jakie znaczenie mają pokazujące się obiekty i jakie są pomiędzy nimi zależności. Sieć na podstawie obserwacji występujących sygnałów stopniowo sama odkrywa, jakie jest ich znaczenie i również sama ustala zachodzące między sygnałami zależności.
Po podaniu do sieci neuronowej każdego kolejnego zestawu sygnałów wejściowych tworzy się w niej pewien rozkład sygnałów wyjściowych - niektóre neurony sieci są pobudzone bardzo silnie, inne słabiej, a jeszcze inne mają sygnały wyjściowe wręcz ujemne. Interpretacja tych zachowań może być taka, że niektóre neurony "rozpoznają" podawane sygnały jako "własne" (czyli takie, które są skłonne akceptować), inne traktują je "obojętnie", zaś jeszcze u innych neuronów wzbudzają one wręcz "awersję".
Po ustaleniu sygnałów wyjściowych wszystkich neuronów w całej sieci - wszystkie wagi wszystkich neuronów są zmieniane, przy czym wielkość odpowiedniej zmiany wyznaczana jest na podstawie iloczynu sygnału wejściowego, wchodzącego na dane wejście neuronu i sygnału wyjściowego produkowanego przez neuron, w którym modyfikujemy wagi. Można to formalnie zapisać w postaci wzoru:
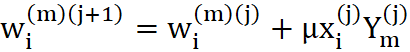
(3.1)
przy czym:
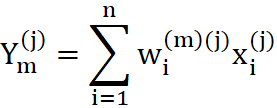
gdzie:
- µ - współczynnik liczbowy decydujący o szybkości uczenia
- y - rzeczywista odpowiedź neuronu na sygnał x
- Podwójne górne indeksy przy współczynnikach wagowych
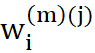 wynikają z faktu, że trzeba uwzględnić numerację neuronów, do których wagi te należą (m) oraz numerację kroków wynikającą z kolejnych pokazów.
wynikają z faktu, że trzeba uwzględnić numerację neuronów, do których wagi te należą (m) oraz numerację kroków wynikającą z kolejnych pokazów.
W efekcie opisanego wyżej algorytmu połączenia między źródłami silnych sygnałów i neuronami które na nie silnie reagują są wzmacniane. Dokładniejsza analiza procesu samouczenia pozwala stwierdzić, że w wyniku konsekwentnego stosowania opisanego algorytmu początkowe, najczęściej przypadkowe "preferencje" neuronów ulegają systematycznemu wzmacnianiu i dokładnej polaryzacji. Jeśli jakiś neuron miał "wrodzoną skłonność" do akceptowania sygnałów pewnego rodzaju - to w miarę kolejnych pokazów nauczy się te sygnały rozpoznawać coraz dokładniej i coraz bardziej precyzyjnie. Po dłuższym czasie takiego samouczenia w sieci powstaną zatem wzorce poszczególnych typów sygnałów występujących na wejściu sieci. W wyniku tego procesu sygnały podobne do siebie będą w miarę postępu uczenia coraz skuteczniej grupowane i rozpoznawane przez pewne neurony, zaś inne typy sygnałów staną się "obiektem zainteresowania" innych neuronów. W wyniku tego procesu samouczenia sieć nauczy się, ile klas podobnych do siebie sygnałów pojawia się na jej wejściach oraz sama przyporządkuje tym klasom sygnałów neurony, które nauczą się je rozróżniać, rozpoznawać i sygnalizować.
Proces samouczenia ma niestety wady. W porównaniu z procesem uczenia z nauczycielem samouczenie jest zwykle znacznie powolniejsze. Co więcej bez nauczyciela nie można z góry określić, który neuron wyspecjalizuje się w rozpoznawania której klasy sygnałów. Stanowi to pewną trudność przy wykorzystywaniu i interpretacji wyników pracy sieci. Co więcej - nie można określić, czy sieć uczona w ten sposób nauczy się wszystkich prezentowanych jej wzorców. Dlatego sieć przeznaczona do samouczenia musi być większa niż sieć wykonująca to samo zadanie, ale trenowana w sposób klasyczny, z udziałem nauczyciela. Szacunkowo sieć powinna mieć co najmniej trzykrotnie więcej elementów warstwy wyjściowej niż wynosi oczekiwana liczba różnych wzorów, które sieć ma rozpoznawać.
Proces uczenia sieci uwalnia nas jednak od uciążliwego tworzenia i zapisywania (w określonym języku programowania) algorytmu wymaganego dla takiego przetwarzania wejściowych danych, by uzyskać pożądany wynik końcowy. Nie odbywa się to jednak za darmo, gdyż ceną, jaką trzeba zapłacić za tę wygodę jest długotrwały i wymagający sporych mocy obliczeniowych proces uczenia. Zwykle jednokrotna prezentacja wszystkich przypadków wchodzących w skład zbioru uczącego (czyli tzw. jedna epoka uczenia) nie wystarcza do osiągnięcia prawidłowego działania sieci. Dlatego też dane uczące prezentowane są wielokrotnie - często kilkaset, kilka tysięcy, albo nawet milionów razy. Co gorsza, proces uczenia jest zawsze procesem indeterministycznym, co oznacza, że wynik uczenia nie jest nigdy całkowicie pewny. Czasami ta sama sieć w tym samym zadaniu może uzyskiwać znacząco różne (co do jakości) rozwiązania postawionego problemu. Fakt ten powoduje, że dla osiągnięcia najlepszego możliwego wyniku proces uczenia trzeba niekiedy powtarzać kilkakrotnie, za każdym razem startując od innych wartości początkowych przyjętych dla współczynników wag. Jest to bardzo kłopotliwe, ale czasami bywa jedynym sposobem pokonania pojawiających się trudności. Na szczęście trudności te nie zawsze występują, co powoduje, że wśród użytkowników sieci neuronowe cieszą się opinią narzędzia sprawnego i wygodnego w użyciu.
Symulacja - modele generujące finansowe strategie inwestycyjne
Po wstępie dotyczącym budowy i uczenia sieci neuronowych, mając już pewne ogólne pojęcie dotyczące tej problematyki można przystąpić do pokazania możliwości zastosowania przedstawionego narzędzia na Giełdzie Papierów Wartościowych do generowania sygnałów kupna/sprzedaży.
Każdy z czytelników może sam we własnym zakresie zbudować model neuronowy do wspomagania podejmowania decyzji inwestycyjnych. Nie jest to zbyt skomplikowane a w Internecie dostępnych jest kilka różnych darmowych programów do tworzenia sieci neuronowych jak chociażby Brain Maker, a dla bardziej zaawansowanych polecam profesjonalne narzędzie firmy Statsoft jakim jest Statistica Neural Networks.
W niniejszym podrozdziale zostaną zaprezentowane trzy modele. Pierwszy model służy do prognozowania pozycji jaką należy zająć na początku danej sesji. Prognozujemy zatem czy nastąpi wzrost/spadek wartości indeksu od otwarcia do zamknięcia sesji w danym dniu.
Początkowo do tworzenia modelu wytypowanych zostało 34 danych wejściowych w skład których wchodziły indeksy różnych giełd, oraz wybrane wskaźniki analizy technicznej. Z tak wstępnie określonej grupy danych wejściowych została wyselekcjonowana podgrupa zmiennych wejściowych mających wartość prognostyczną. Selekcja przeprowadzona została metodą prób i błędów, przy zastosowaniu sieci o radialnych funkcjach bazowych, która osiąga minimum globalne funkcji błędu, a zatem daje powtarzalne wyniki. Do tworzenia modeli neuronowych analizowanych w dalszej części tego rozdziału wybrane zostały zatem te dane, które poprawiały uzyskiwany wynik i nie wprowadzały nadmiernych szumów.
Te dane to:
- WIG20 O, WIG20 O t-1, WIG20 O t-2 - wartość indeksu WIG20 na otwarciu w chwili t, oraz t-1 i t-2
- WIG20 H - maksymalna wartość indeksu na danej sesji
- WIG20 L - minimalna wartość indeksu na danej sesji
- WIG20 C, WIG20 C t-1, WIG20 C t-2, WIG20 C t-3, - wartość indeksu WIG20 na zamknięciu sesji w czasie t, t-1, t-2, t-3
- ROC - Rate Of Change - wskaźnik zmian - Jest to wskaźnik impetu mierzący wielkość zmiany ceny w zadanym okresie. Kierunek notowań powinien być potwierdzony analogiczną tendencją wskaźnika. Jeżeli wskaźnik osiąga nowe minimum i zaczyna rosnąć jest to wstępny sygnał kupna, osiągnięcie nowego szczytu i następujący po nim spadek jest wstępnym sygnałem sprzedaży
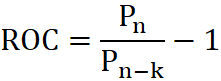
(3.7)
gdzie:
- Pn-k to kurs sprzed k notowań.
- obrót w mln PLN oraz średnia obrotu z 5 okresów w mln PLN
- RSI 9, RSI 14 - Relative Strenght Index - indeks siły względnej - Jest to jeden z najpopularniejszych i najczęściej używanych oscylatorów. Nie jest to jednak, jak wskazuje nazwa, typowy miernik siły względnej. Jak klasyczny oscylator zyskuje wartości w przedziale 0 -100. Podstawowa analiza zakłada poszukiwanie dywergencji względem wykresu cenowego. RSI jest również miernikiem stanów wykupienia/wyprzedania rynku. Wartości powyżej 70 pkt., są odbierane jako wykupienie rynku, poniżej 30 pkt. jako wyprzedanie rynku
- linii trendów, poszukiwaniu formacji cenowych oraz sygnały płynące z ich przebicia
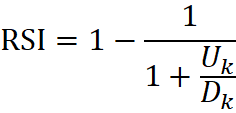
(3.8)
gdzie:
- Uk - średni wzrost kursu zk sesji, a Dk to średni spadek kursu zk sesji.
- MA 4, MA 9, MA 18 - średnia z wartości indeksu WIG20 na zamknięciu z odpowiednio 4, 9, 18 kolejnych sesji
- WIG O - wartość indeksu WIG na otwarciu
- WIG C - wartość indeksu WIG na zamknięciu sesji
- NASDAQ O
- NASDAQ C, NASDAQ C t-1, NASDAQ C t-2 - wartość indeksu NASDAQ na zamknięciu sesji w czasie t, oraz t-1 i t-2
- S&P 500 O
- S&P 500 C
W pierwszym modelu możliwe jest wystąpienie 3 stanów:
- pozycja długa - kupno na otwarciu sesji,
- pozycja krótka - sprzedaż na otwarciu sesji
- poza rynkiem - wstrzymanie się z kupnem i sprzedażą na danej sesji. Ta opcja występuje wówczas, gdy zmiana wartości indeksu jest mniejsza od założonej pewnej punktowej wartości indeksu (w tabeli jako parametr "x").
Parametr "x" określa jaka duża musi być punktowa zmiana wartości indeksu, aby zająć odpowiednią pozycję na otwarciu giełdy innej niż "poza rynkiem". Określa zatem, jakie musi być minimalne wahanie indeksu na danej sesji, aby pojawił się sygnał kupna lub sprzedaży.
Te trzy możliwe do wystąpienia stany tworzą wektor danych wyjściowych (dane wzorcowe).
W niniejszym modelu mamy do czynienia z klasyfikacją - na podstawie danych wejściowych, ustalamy jeden z trzech stanów na kolejną sesję. Przy problemach klasyfikacji dobre rezultaty przynosi zastosowanie sieci RBF, a jej zaletą jest powtarzalność i uzyskiwanie minimów globalnych. Do budowy modelu została użyta sieć neuronowa RBF o 192 neuronach radialnych. Wektor danych wejściowych składał się z 962 danych treningowych i 250 walidacyjnych.
Uzyskane rezultaty obrazują poniższe tabele.
Tabela 4.1 Hipotetyczny zysk z inwestycji w indeks WIG20 w zależności od parametru "X"
10
5 lat
1 rok
100 sesji
22.208
695
505
9
5 lat
1 rok
100 sesji
23.467
1.754
664
8
5 lat
1 rok
100 sesji
26.969
2.435
699
7
5 lat
1 rok
100 sesji
28.908
2.612
822
6
5 lat
1 rok
100 sesji
30.020
1.785
543
5
5 lat
1 rok
100 sesji
22.232
962
420
4
5 lat
1 rok
100 sesji
20.995
543
340
3
5 lat
1 rok
100 sesji
21.828
930
315
2
5 lat
1 rok
100 sesji
21.670
691
456
1
5 lat
1 rok
100 sesji
20.034
-151
142
0
5 lat
1 rok
100 sesji
18.927
-483
-3
| X | 5 lat | 1 rok | 100 sesji |
|---|---|---|---|
| 10 | 22.208 | 695 | 505 |
| 9 | 23.467 | 1.754 | 664 |
| 8 | 26.969 | 2.435 | 699 |
| 7 | 28.908 | 2.612 | 822 |
| 6 | 30.020 | 1.785 | 543 |
| 5 | 22.232 | 962 | 420 |
| 4 | 20.995 | 543 | 340 |
| 3 | 21.828 | 930 | 315 |
| 2 | 21.670 | 691 | 456 |
| 1 | 20.034 | -151 | 142 |
| 0 | 18.927 | -483 | -3 |
W tabeli nr 4.1 zobrazowany jest hipotetyczny zysk z inwestycji w indeks WIG20, po uwzględnieniu prowizji w wysokości 15 pln (30 pln w trakcie 1 sesji) za zajęcie pozycji zgodne z prognozą uzyskaną przy pomocy sieci neuronowej. Optymalny zysk osiągany jest przy parametrze "x" równym 6 i 7. Jest to niestety tylko czysto teoretyczne podejście, przy założeniu, że istnieje instrument o cechach kontraktu terminowego, ale o wartości całkowicie zgodnej z wartością indeksu. Jest to zatem założenie czysto teoretyczne, co sprawia, że wynik z inwestycji w WIG20 nie ma wartości merytorycznej, a jedynie czysto poglądową.
Istnieje jednak alternatywa dla takiego sposobu przeprowadzania transakcji mianowicie kupno lub sprzedaż kontraktów terminowych na indeks WIG20. Inwestowanie, a w zasadzie spekulacja przy pomocy kontraktów terminowych daje inwestorowi możliwość uzyskania dużo wyższej stopy zwrotu niż w przypadku inwestowania w akcje, gdyż inwestor spekulujący na kontraktach korzysta z dźwigni finansowej.
Tabela 4.2 Wynik z inwestycji w kontrakty futures na WIG20 w zależności od parametru "x".
10
3 lata
2 lata
1 rok
100 sesji
968
3464
1086
938
9
3 lata
2 lata
1 rok
100 sesji
-3274
1488
231
1215
8
3 lata
2 lata
1 rok
100 sesji
61
3732
774
938
7
3 lata
2 lata
1 rok
100 sesji
4470
7700
1880
1770
6
3 lata
2 lata
1 rok
100 sesji
4364
6285
1727
1030
5
3 lata
2 lata
1 rok
100 sesji
-370
2363
842
1506
4
3 lata
2 lata
1 rok
100 sesji
-365
1879
-173
-885
3
3 lata
2 lata
1 rok
100 sesji
-1520
494
-930
-2959
2
3 lata
2 lata
1 rok
100 sesji
-2858
-185
-886
-2800
1
3 lata
2 lata
1 rok
100 sesji
-4125
-1189
-1687
-4385
0
3 lata
2 lata
1 rok
100 sesji
-4282
-1246
-1293
-3381
| X | 3 lata | 2 lata | 1 rok | 100 sesji |
|---|---|---|---|---|
| 10 | 968 | 3464 | 1086 | 938 |
| 9 | -3274 | 1488 | 231 | 1215 |
| 8 | 61 | 3732 | 774 | 938 |
| 7 | 4470 | 7700 | 1880 | 1770 |
| 6 | 4364 | 6285 | 1727 | 1030 |
| 5 | -370 | 2363 | 842 | 1506 |
| 4 | -365 | 1879 | -173 | -885 |
| 3 | -1520 | 494 | -930 | -2959 |
| 2 | -2858 | -185 | -886 | -2800 |
| 1 | -4125 | -1189 | -1687 | -4385 |
| 0 | -4282 | -1246 | -1293 | -3381 |
W tabeli 4.2 zestawiony został wynik finansowy z inwestycji w kontrakty terminowe po odjęciu prowizji w wysokości 15 pln za kupno/sprzedaż 1 kontraktu, przy założeniu braku reinwestycji zysków. Maksymalny horyzont inwestycji w tym przypadku wynosi 3 lata.
Podobnie jak w tabeli 4.1 optymalne zyski przynosi prognozowanie pozycji "krótka/długa" przy zmienności wynoszącej 6 i 7.
Jak widać z powyższego zestawienia niniejszy model pozwala na całkiem przyzwoity zysk poprzez spekulacyjną grę na kontraktach futures w oparciu o sygnały generowane poprzez sieć neuronową. Inwestor grający w oparciu o ten model neuronowy mógł uzyskać w okresie 18-06-2002 do 06-11-2002 1770 pln, a w przeciągu roku (06-11-2001 do 06-11-2002) 1880 pln, przy założeniu braku reinwestycji zysku (czyli grze tylko przy pomocy 1 kontraktu). Jest to bardzo wysoki zwrot z zainwestowanego kapitału, gdyż w przypadku kontraktów terminowych blokowany jest na rachunku praw pochodnych depozyt zabezpieczający w wysokości ok. 8% wartości indeksu, co daje zwrot w wysokości 200-250% rocznie.
Drugim modelem zaprezentowanym w niniejszym artykule jest sieć neuronowa, której zadaniem jest prognozowanie krótkoterminowego trendu na giełdzie. Model ten daje całkiem przyzwoite rezultaty, a tym, co różni go od poprzedniego, jest właśnie prognozowanie trendu, a nie zmiany wartości indeksu na 1 sesji. Dane wejściowe są takie jak poprzednio.
Możliwe jest wystąpienie 2 stanów, stanowiących wzorzec danych wyjściowych:
- pozycja długa - kupno na otwarciu sesji,
- pozycja krótka - sprzedaż na otwarciu sesji.
W tym modelu jednak dana pozycja jest utrzymywana również po zamknięciu sesji (pozwala to zmniejszyć wartość prowizji), aż do wygenerowania przez sieć neuronową sygnału pozycji przeciwstawnego do aktualnie zajmowanego.
Wzorzec danych wyjściowych został utworzony poprzez subiektywną analizę wykresów obrazujących wartości indeksu WIG20.
Do uczenia sieci zostało użytych 1497 przypadków, z czego 1177 to dane uczące, a 320 dane walidacyjne wyznaczane w sposób losowy. Dane pochodzą z okresu od 02-01-1997 do 31-12-2002.
Przy budowie tego modelu, zostały przeanalizowane trzy rodzaje sieci neuronowych: Perceptronowa, Liniowa i Sieć o radialnych funkcjach bazowych. Wyniki zawarte są w poniższej tabeli.
Tabela 4.3.1 Wynik z inwestycji w WIG20 i kontrakty futures na WIG20 w zależności od zastosowanej sieci neuronowej, z uwzględnieniem prowizji od każdej transakcji w wysokości 15 PLN
Liniowa sieć neuronowa CCL=0,5
6 lat
2 lata
1 rok
-501
-7.046
-4.244
Liniowa sieć neuronowa CCL=0,46
6 lat
2 lata
1 rok
-4.729
-8.573
-7.470
MLP CCL=0,5
6 lat
2 lata
1 rok
6.138
-3.571
-6.572
MLP CCL=0,46
6 lat
2 lata
1 rok
8.525
-2.575
-3.901
RBF CCL=0,5
6 lat
2 lata
1 rok
72.993
8.498
4.496
RBF CCL=0,46
6 lat
2 lata
1 rok
68.513
7.516
3.725
| 6 lat | 2 lata | 1 rok | |
|---|---|---|---|
| Liniowa sieć neuronowa CCL=0,5 | -501 | -7.046 | -4.244 |
| Liniowa sieć neuronowa CCL=0,46 | -4.729 | -8.573 | -7.470 |
| MLP CCL=0,5 | 6.138 | -3.571 | -6.572 |
| MLP CCL=0,46 | 8.525 | -2.575 | -3.901 |
| RBF CCL=0,5 | 72.993 | 8.498 | 4.496 |
| RBF CCL=0,46 | 68.513 | 7.516 | 3.725 |
Tabela 4.3.2 Wynik z inwestycji w WIG20 i kontrakty futures na WIG20 w zależności od zastosowanej sieci neuronowej, z uwzględnieniem prowizji od każdej transakcji w wysokości 15 PLN
Liniowa sieć neuronowa CCL=0,5
3 lata
2 lata
1 rok
-21.780
-18.100
-10.380
Liniowa sieć neuronowa CCL=0,46
3 lata
2 lata
1 rok
-35.265
-33.615
-24.335
MLP CCL=0,5
3 lata
2 lata
1 rok
-784
-4.652
-7.392
MLP CCL=0,46
3 lata
2 lata
1 rok
-8.025
-19.035
-16.035
RBF CCL=0,5
3 lata
2 lata
1 rok
12.402
9.045
5.100
RBF CCL=0,46
3 lata
2 lata
1 rok
23.025
14.522
8.873
| 3 lata | 2 lata | 1 rok | |
|---|---|---|---|
| Liniowa sieć neuronowa CCL=0,5 | -21.780 | -18.100 | -10.380 |
| Liniowa sieć neuronowa CCL=0,46 | -35.265 | -33.615 | -24.335 |
| MLP CCL=0,5 | -784 | -4.652 | -7.392 |
| MLP CCL=0,46 | -8.025 | -19.035 | -16.035 |
| RBF CCL=0,5 | 12.402 | 9.045 | 5.100 |
| RBF CCL=0,46 | 23.025 | 14.522 | 8.873 |
Najgorsze wyniki przynosi liniowa sieć neuronowa, co zapewne wiąże się z jej specyfiką (liniowa sieć neuronowa, jako najprostsza swoją budową dobrze radziłaby sobie z zależnościami liniowymi, a rynek akcji z pewnością rządzi się nieliniowymi zależnościami o trudnym do odgadnięcia charakterze). W przypadku sieci perceptronowej wyniki są lepsze od tych uzyskanych przy pomocy liniowej sieci neuronowej, ale są całkowicie nieprzydatne ze względu na straty, jakie przynoszą. Należy pamiętać tutaj również, iż inwestycja w WIG20 jest inwestycją czysto hipotetyczną, przy założeniu, że istnieje instrument o cechach kontraktu terminowego, ale o wartości równej wartości indeksu. Jest to oczywiście założenie czysto teoretyczne, co sprawia, że wynik z inwestycji w WIG20 nie ma wartości merytorycznej, a jedynie czysto poglądową. Drugie zestawienie dotyczące inwestycji w kontrakty terminowe na WIG20 są w pełni zgodne z rzeczywistością.
Zupełnie inaczej wygląda sytuacja przy zastosowaniu sieci neuronowych o radialnych funkcjach bazowych. Tutaj bez względu na okres inwestycji osiągamy przyzwoite zyski. Warto porównać maksymalne zyski z bieżącego modelu z maksymalnymi zyskami osiągniętymi w modelu poprzednim. Zestawienie zysków przedstawia się następująco:
Tabela 4.4 Zestawienie maksymalnych zysków dla modelu bieżącego i poprzedniego przy inwestowaniu w kontrakty futures na WIG20
Model poprzedni
3 Lata
2 Lata
1 Rok
4.470
7.700
1.880
Model bieżący
3 Lata
2 Lata
1 Rok
23.025
14.522
8.873
| 3 Lata | 2 Lata | 1 Rok | |
|---|---|---|---|
| Model poprzedni | 4.470 | 7.700 | 1.880 |
| Model bieżący | 23.025 | 14.522 | 8.873 |
Jak widać z tabeli 4.4 maksymalny średni możliwy do uzyskania zysk z bieżącego modelu jest od 2 (dla horyzontu inwestycji 2 lata) do przeszło 5 (dla horyzontu inwestycji 3 lata) razy większy niż w modelu poprzednim.
Parametr CCL, który widnieje w tabeli 4.3 to tzw. Classification Confidence Level (poziom ufności). Służy on do translacji odpowiedzi neuronu z postaci numerycznej do odpowiedniej klasy. Przykładowo: dla poziomu ufności 0,46 przypadki na wyjściu pomiędzy 0,54 a 0,46 klasyfikowane są jako nieznane, a pozostałe klasyfikowane do odpowiedniej klasy. Standardowo program Statistica Neural Networks poziom ufności ustala na poziomie 0,05, ale w takim przypadku, przy problemie inwestycji na giełdzie sieć neuronowa nie jest w stanie dokonać klasyfikacji danych do odpowiednich klas, a prawie wszystkie odpowiedzi mają status "nieznany", czyli niemożliwy do zaklasyfikowania do odpowiedniej klasy.
Tabela 4.5.1 Klasyfikacja przypadków dla poziomu ufności 0,5
Total
Dane uczące, d
Dane uczące, k
582
597
Correct
Dane uczące, d
Dane uczące, k
432
439
Wrong
Dane uczące, d
Dane uczące, k
150
158
Unknown
Dane uczące, d
Dane uczące, k
0
0
d
Dane uczące, d
Dane uczące, k
432
158
k
Dane uczące, d
Dane uczące, k
150
439
| Dane uczące, d | Dane uczące, k | |
|---|---|---|
| Total | 582 | 597 |
| Correct | 432 | 439 |
| Wrong | 150 | 158 |
| Unknown | 0 | 0 |
| d | 432 | 158 |
| k | 150 | 439 |
Tabela 4.5.2 Klasyfikacja przypadków dla poziomu ufności 0,5
Total
Dane walidacyjne, d
Dane walidacyjne, k
138
182
Correct
Dane walidacyjne, d
Dane walidacyjne, k
80
106
Wrong
Dane walidacyjne, d
Dane walidacyjne, k
58
76
Unknown
Dane walidacyjne, d
Dane walidacyjne, k
0
0
d
Dane walidacyjne, d
Dane walidacyjne, k
80
76
k
Dane walidacyjne, d
Dane walidacyjne, k
58
106
| Dane walidacyjne, d | Dane walidacyjne, k | |
|---|---|---|
| Total | 138 | 182 |
| Correct | 80 | 106 |
| Wrong | 58 | 76 |
| Unknown | 0 | 0 |
| d | 80 | 76 |
| k | 58 | 106 |
Tabela 4.6.1 Klasyfikacja przypadków dla poziomu ufności 0,46
Total
Dane uczące, d
Dane uczące, k
582
597
Correct
Dane uczące, d
Dane uczące, k
388
390
Wrong
Dane uczące, d
Dane uczące, k
112
116
Unknown
Dane uczące, d
Dane uczące, k
82
91
d
Dane uczące, d
Dane uczące, k
388
116
k
Dane uczące, d
Dane uczące, k
112
390
| Dane uczące, d | Dane uczące, k | |
|---|---|---|
| Total | 582 | 597 |
| Correct | 388 | 390 |
| Wrong | 112 | 116 |
| Unknown | 82 | 91 |
| d | 388 | 116 |
| k | 112 | 390 |
Tabela 4.6.2 Klasyfikacja przypadków dla poziomu ufności 0,46
Total
Dane walidacyjne, d
Dane walidacyjne, k
138
182
Correct
Dane walidacyjne, d
Dane walidacyjne, k
75
92
Wrong
Dane walidacyjne, d
Dane walidacyjne, k
49
56
Unknown
Dane walidacyjne, d
Dane walidacyjne, k
14
34
d
Dane walidacyjne, d
Dane walidacyjne, k
75
56
k
Dane walidacyjne, d
Dane walidacyjne, k
49
92
| Dane walidacyjne, d | Dane walidacyjne, k | |
|---|---|---|
| Total | 138 | 182 |
| Correct | 75 | 92 |
| Wrong | 49 | 56 |
| Unknown | 14 | 34 |
| d | 75 | 56 |
| k | 49 | 92 |
Na koniec niniejszego opracowania zaproponowana zostanie metoda generowania strategii transakcyjnych, wykorzystująca sieć neuronową Kohonena (SOM) jako narzędzie wstępnego grupowania wektorów wartości wejściowych, opisujących stan rynku akcji. Jest to podejście odmienne od poprzednich modeli, gdyż wykorzystuje sieć uczoną w sposób nienadzorowany. Metoda wykorzystuje właściwości sieci SOM jako narzędzia realizującego nieliniowe przekształcenie dowolnej przestrzeni metrycznej w przestrzeń dyskretną, a także nieparametryczną regresję dokonującą dopasowania skończonej liczby wektorów kodowych (wektorów wag neuronów mapy) do rozkładu obiektów w przestrzeni cech. Wykorzystanie tych właściwości jest szczególnie uzasadnione w zagadnieniu analizy rynków finansowych. W istocie sieci SOM dość często używa się w zagadnieniu identyfikacji skupień wzorców (formacji) generowanych przez finansowe szeregi czasowe i możliwych do zaobserwowania na ich wykresach, oraz do identyfikacji typowych wzorców (zob. np. [4],[12]).
Główna idea metody jest następująca:
- W oparciu o ciąg uczący (obejmujący historyczne notowania danego waloru z pewnego okresu i zawierający zmienne istotne z punktu widzenia opisu stanu dynamiki notowań) realizowany jest proces grupowania wzorców (wektorów), opisujących stan rynku w poszczególnych chwilach czasowych (sesjach giełdowych). Po zakończeniu procesu uczenia sieci SOM (grupowania) pewne neurony mapy reprezentują związane z nimi skupienia (klastry) wzorców.
- Dokonywana jest analiza przyszłych stóp zwrotu uzyskanych dla wzorców należących do każdej grupy osobno, analiza ta obejmuje obliczenie średniej przyszłej stopy zwrotu dla wzorców z danej klasy oraz obliczenie pewnego przyjętego wskaźnika będącego miarą ryzyka inwestycyjnego; wskaźnikiem takim może być np. odchylenie standardowe przyszłych stóp zwrotu dla rozważanej klasy.
- Na podstawie analizy otrzymanych dla każdej klasy wskaźników zysku i ryzyka, a także w oparciu o indywidualne preferencje inwestora (dotyczące np. poziomu akceptowalnego ryzyka), z każdą grupą wzorców kojarzona jest określona decyzja inwestycyjna, np. kup, sprzedaj, utrzymuj pozycję inwestycyjną.
- W trybie realizacji (wykorzystania) skonstruowanego modelu, zakwalifikowanie pojawiającego się nowego wzorca opisującego bieżącą dynamikę rynku danego waloru do określonej klasy jednoznacznie determinuje decyzję inwestycyjną; model taki jest więc funkcjonalnym modelem decyzyjnym realizującym określoną strategię inwestycyjną.
Poniżej zostały przedstawione wyniki badań efektywności modelu decyzyjnego zbudowanego według zaproponowanej metody, w zagadnieniu realizacji strategii inwestycyjnej dla akcji spółki KGHM w przyjętym okresie czasu. Zadaniem modelu było generowanie decyzji inwestycyjnej (na podstawie analizy bieżącej sytuacji rynkowej) dla okresu od zamknięcia notowań w dniu bieżącym (moment realizacji decyzji) do zamknięcia notowań podczas kolejnej sesji giełdowej (kiedy może zostać zrealizowana następna transakcja). W trakcie realizacji aktywnej strategii inwestycyjnej założono możliwość realizacji dwóch typów transakcji: kupna akcji za całość posiadanych w portfelu środków, oraz krótkiej sprzedaży akcji o wartości równej posiadanych w portfelu środków (bez możliwości zajmowania pozycji pośrednich)[2].
Wykorzystane w badaniach dane obejmowały notowania (kursy zamknięcia) spółki KGHM w okresie od 10.07.1997 do 21.11.2003. Jako dane wejściowe dla modelu przyjęto (arbitralnie) 13 zmiennych, których wartości w poszczególnych dniach obliczono na podstawie notowań akcji. Zestaw zmiennych wejściowych zawierał: cztery ostatnie logarytmiczne jednodniowe stopy zwrotu, dwie kolejne ostatnie logarytmiczne dwudniowe stopy zwrotu, nachylenia pięciodniowego trendu[3] kursu: obecne i sprzed czterech dni, obecne nachylenie dziesięciodniowego trendu, dynamikę zmiany logarytmicznych jednodniowych stóp zwrotu (różnicę tych stóp), dynamikę zmiany logarytmicznych dwudniowych stóp zwrotu, dynamikę zmiany pięciodniowego trendu (różnicę wskaźników trendu obecnego i sprzed 4 dni), oraz różnicę między nachyleniem trendu 5-dniowego i 10-dniowego.
Łącznie (po pominięciu notowań niezbędnych do obliczenia wartości początkowych wszystkich zmiennych) wyodrębniono 1573 wzorce, z czego pierwsze 951 wektorów utworzyło zbiór uczący, a ostatnie 622 wzorce zaliczono do zbioru testowego (przeznaczonego do końcowego testowania i oceny efektywności modelu). Podział danych na uczące i testowe zrealizowano przy uwzględnieniu proporcji (w przybliżeniu) 60% / 40% oraz w taki sposób, aby całkowite stopy zwrotu dla obu tych okresów wynosiły w przybliżeniu 0. Kurs akcji KGHM w okresie obejmującym dane uczące oraz testowe zaprezentowano na rys. 3.
Rys. 3. Kurs akcji KGHM w okresie zawierającym dane uczące oraz testowe.
Źródło: opracowanie własne.
Dobierając parametry struktury i uczenia sieci SOM przyjęto sieć zawierającą 16 neuronów na dwuwymiarowej mapie o wymiarach 4 ? 4, euklidesową metrykę określająca odległość między wektorami w przestrzeni cech, oraz współczynnik uczenia równy 0,6 i malejący wraz z upływem czasu uczenia. Przyjęto 50 epok uczenia. Rozmiar sąsiedztwa ustalono na początku procesu uczenia na maksymalny (obejmujący wszystkie neurony), ale malejący liniowo podczas uczenia do zera (dla 50 epoki). Zastosowano standaryzację zmiennych wejściowych poprzez taką transformację, aby średnia (dla zbioru uczącego) wynosiła zero, a odchylenie standardowe: jeden. Wektory wag początkowych sieci określono jako losowo wybrane wektory wejściowe z ciągu uczącego.
Po przeprowadzeniu procesu uczenia sieci zaobserwowano, iż liczba wzorców ze zbioru uczącego przyporządkowana poszczególnym neuronom mapy (tzn. wektorów, dla których dany neuron stał się neuronem zwycięskim) waha się pomiędzy 41 a 76. Przyjęto zatem, iż każdy neuron reprezentuje osobne skupienie (grupę) wzorców (chociaż sąsiednie obszary mapy mogą odwzorowywać podobne wzorce), a zatem liczba tych grup jest równa 16. Obliczone dla zbioru uczącego istotne wskaźniki charakteryzujące poszczególne grupy, takie jak: liczba wzorców n, średnia przyszła logarytmiczna jednodniowa stopa zwrotu r (pomnożona przez 1000), oraz odchylenie standardowe dla tych stóp zwrotu? (pomnożone przez 1000) przedstawiono w tabeli 4.7.
W celu powiązania z każdą grupą wzorców określonej decyzji inwestycyjnej przyjęto, iż podstawę tej decyzji stanowić będzie wartość wskaźnika s przedstawiająca stosunek stopy zwrotu do ryzyka dla wzorców danej grupy (miarą ryzyka jest odchylenie standardowe stóp zwrotu). W istocie s to powszechnie używany w analizie finansowej wskaźnik Sharpe'a przy założeniu, iż stopa procentowa aktywów wolnych od ryzyka wynosi zero. Wskaźnik ten jest często wykorzystywaną przez inwestorów miarą efektywności inwestycji w dany walor, uwzględnia bowiem powiązane ze sobą dwa podstawowe czynniki decyzyjne: oczekiwany zysk oraz ryzyko. W niniejszych badaniach założono, iż jeśli wartość bezwzględna tego wskaźnika przekracza określoną wielkość (przyjęto 10%), stanowi to podstawę do podjęcia decyzji kupna (gdy s>0,1) lub krótkiej sprzedaży waloru (gdy s<- 0,1); w przeciwnym przypadku należy utrzymać bieżącą pozycję inwestycyjną bez zmian. Tą regułę decyzyjną można więc wyrazić formułą:
- Jeżeli s> 10% (a akcje są krótko sprzedane) to dokonaj kupna akcji (K),
- Jeżeli s < -10% (a akcje są kupione) to dokonaj krótkiej sprzedaży akcji (S),
- W przeciwnym przypadku utrzymaj bieżącą pozycję inwestycyjną bez zmian (T).
Wartości współczynnika s (dla danych uczących), oraz związane z nimi decyzje inwestycyjne przyporządkowane do poszczególnych klas wzorców zidentyfikowanych przez sieć SOM, umieszczono również w tabeli 4.7.
Tabela 4.7. Wartości podstawowych wskaźników (obliczonych dla zbioru uczącego) oraz wynikających z nich decyzji inwestycyjnych dla poszczególnych grup wzorców
1
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
61
-4,3
34,1
-12,5%
S
2
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
41
-4,1
42,1
-9,8%
T
3
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
47
-0,5
32,0
-1,7%
T
4
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
54
4,8
26,7
18,0%
K
5
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
51
9,3
25,8
36,1%
K
6
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
71
2,8
21,6
13,0%
K
7
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
72
-7,9
24,2
-32,7%
S
8
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
60
0,7
29,6
2,4%
T
9
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
53
7,2
24,9
29,1%
K
10
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
73
-1,0
29,7
-3,5%
T
11
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
76
-3,7
28,1
-13,2%
S
12
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
67
-2,1
30,8
-6,9%
T
13
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
51
3,9
40,1
9,7%
T
14
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
54
1,1
28,9
3,8%
T
15
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
56
-2,7
32,8
-8,2%
T
16
Liczba wzorców
n
Śr. log. stopa zwrotu r*1000
Odch. std.
*1000
s = r/odch. std
Decyzja
64
1,7
54,4
3,1%
T
| Nr grupy (neuronu SOM) | Liczba wzorców n | Śr. log. stopa zwrotu r*1000 | Odch. std. *1000 |
s = r/odch. std | Decyzja |
|---|---|---|---|---|---|
| 1 | 61 | -4,3 | 34,1 | -12,5% | S |
| 2 | 41 | -4,1 | 42,1 | -9,8% | T |
| 3 | 47 | -0,5 | 32,0 | -1,7% | T |
| 4 | 54 | 4,8 | 26,7 | 18,0% | K |
| 5 | 51 | 9,3 | 25,8 | 36,1% | K |
| 6 | 71 | 2,8 | 21,6 | 13,0% | K |
| 7 | 72 | -7,9 | 24,2 | -32,7% | S |
| 8 | 60 | 0,7 | 29,6 | 2,4% | T |
| 9 | 53 | 7,2 | 24,9 | 29,1% | K |
| 10 | 73 | -1,0 | 29,7 | -3,5% | T |
| 11 | 76 | -3,7 | 28,1 | -13,2% | S |
| 12 | 67 | -2,1 | 30,8 | -6,9% | T |
| 13 | 51 | 3,9 | 40,1 | 9,7% | T |
| 14 | 54 | 1,1 | 28,9 | 3,8% | T |
| 15 | 56 | -2,7 | 32,8 | -8,2% | T |
| 16 | 64 | 1,7 | 54,4 | 3,1% | T |
Tak zdeterminowaną aktywną strategię inwestycyjną zastosowano następnie w okresie obejmującym dane testowe (przy założeniu początkowej wartości portfela równej 1000). Zgodnie z przyjętym założeniem inwestor (bazujący na zbudowanym modelu) mógł zajmować jedynie dwa rodzaje pozycji inwestycyjnych: kupić akcje (za całość posiadanych aktualnie środków finansowych), oraz krótko sprzedać akcje (o wartości całego portfela w chwili sprzedaży). Wobec takich założeń model może generować zysk niezależnie od kierunku zmiany cen akcji (pod warunkiem trafnych decyzji) lub - w przypadku błędnych decyzji - przynosić straty.
Model zastosowany do danych w okresie testowym wygenerował poprawne decyzje w 55,95% przypadków. Okazuje się jednak, że ten wynik jest bardzo dobry przy założeniu, że generowane są poprawne decyzje w kluczowych momentach poprzedzających znaczne ruchy cen. Rzeczywistą efektywność modelu potwierdzają bowiem wyniki finansowe: na końcu okresu obejmującego dane testowe osiągnięto końcową wartość portfela (przy założeniu zerowej prowizji maklerskiej) równą 5065, to znaczy uzyskano całkowitą stopę zwrotu wynoszącą 406,5% (wobec zerowej stopy zysku w przypadku pasywnej inwestycji w akcje KGHM w tym okresie). Ten wynik jest lepszy niż w przypadku klasycznego zastosowania sieci neuronowych typu perceptron w analogicznym zagadnieniu. Również w przypadku przyjęcia niezerowej prowizji maklerskiej, pobieranej przy zmianie pozycji inwestycyjnej z krótkiej na długą lub odwrotnie i wynoszącej 0,2% wartości aktywów portfela (co jest wielkością realną na rynku) uzyskano wysoką stopę zwrotu wynoszącą 292,8% (na ograniczenie kosztów wynikających z prowizji maklerskiej duży wpływ ma częste stosowanie decyzji typu "utrzymaj bieżącą pozycję" (T) co ogranicza znacznie liczbę transakcji).
Przebieg zmian wartości portfela dla rozważanej aktywnej strategii inwestycyjnej (w porównaniu do pasywnej inwestycji polegającej na kupnie i utrzymywaniu portfela akcji przez cały okres) dla danych testowych przedstawiono na rys 4.
Rys. 4. Wartość portfela w czasie w okresie testowym przy zastosowaniu trzech strategii inwestycyjnych: pasywnej, aktywnej opartej o decyzje analizowanego modelu przy zerowej prowizji maklerskiej, oraz aktywnej jw. przy prowizji wynoszącej 0,2%.
Źródło: obliczenia własne.
Podsumowanie
Otrzymane wyniki z przedstawionych w artykule modeli wspomagających decyzje inwestycyjne świadczą o wysokiej efektywności rozważanych metod. Do dodatkowych zalet zaliczyć można elastyczność dostosowania parametrów strategii decyzyjnej modelu do indywidualnych preferencji inwestora (np. dotyczących ryzyka inwestycyjnego), a także możliwość zróżnicowanego doboru danych wejściowych.
Radomir Domaradzki
doktorant Akademii Górniczo-Hutniczej w Krakowie, absolwent Akademii Ekonomicznej w Krakowie
Fragment recenzji Prof. dr hab. inż. Ryszarda Tadeusiewicza:
Opiniowany artykuł pokazuje możliwości zastosowania nowoczesnego narzędzia informatycznego, jakim są sztuczne sieci neuronowe, do wspomagania decyzji inwestycyjnych. Opracowanie zawiera przejrzyste wprowadzenie do zagadnienia sztucznych sieci neuronowych, opisuje w czytelny i zrozumiały sposób sposoby ich uczenia oraz prezentuje przykłady użycia różnych typów sieci neuronowych. Ze względu na przewidywany profil zainteresowań osób odwiedzających portal bossa.pl przykłady zastosowań sieci neuronowych skoncentrowano głównie na problematyce generowania strategii transakcyjnych (sygnałów kupna/sprzedaży) oraz prognozowania krótkoterminowych trendów na rynkach kapitałowych. Praca w sporej części ma charakter przeglądowy i oparta jest na danych literaturowych (w bibliografii przywołano 21 pozycji literatury - dobrze dobranych i poprawnie cytowanych), jednak w drugiej jej części Autor przedstawia wyniki własnych badań związanych ze stosowaniem sieci neuronowych jako narzędzia do prognozowania szeregów czasowych oraz przedstawia własne oryginalne wyniki naukowe, uzyskane na przykładzie danych uzyskanych z Giełdy Papierów Wartościowych w Warszawie.
Praca jest poprawna w sensie wiedzy teoretycznej, jaką w niej Autor prezentuje, a także zawiera elementy oryginalne, pochodzące ze wskazanych wyżej oryginalnych badań, jakie mgr Domaradzki prowadził przez kilka lat w celu ustalenia możliwości oraz ograniczeń sieci neuronowych traktowanych jako narzędzia prognostyczne dla potrzeb wspomagania decyzji inwestycyjnych. Moim zdaniem opublikowanie pracy jest możliwe i zdecydowanie celowe, a skutek tej publikacji będzie niewątpliwie pozytywny, wywoła bowiem wzrost zainteresowania ważną i ciekawą dziedziną sieci neuronowych.
Literatura
- Barr, D.S., Mani G.:"Using Neural Nets to Manage Investments", AI Expert pp. 16-21, 1994.
- Beltratti A., Margarita S., Terna P.: "Neural Networks for Economic and Financial Modelling", ITCP, London, 1996.
- Berry M.J.A., Linoff G.S.:"Mastering data mining", John Wiley & Sons, New York, 2000.
- Deboeck G.:"Investment Maps of Emerging Markets", in Deboeck G. and Kohonen T.:"Visual Explorations in Finance", Springer 1997, pp. 83-105, 1997.
- Domaradzki R.:"Sieci neuronowe w predykcji i prognozowaniu", AE w Krakowie, Praca magisterska, Kraków 2003.
- Duch W., Korbicz J., Rutkowski L., Tadeusiewicz R. "Biocybernetyka i inżynieria biomedyczna 2000", Tom 6"Sieci neuronowe", Akademicka Oficyna Wydawnicza, Warszawa 2000.
- Haefke C., Helmenstein C.""Neural Networks in the Capital Markets: An Application to Index Forecasting", Computational Economics, pp. 37-50, 1996.
- Hastie T., Tibshirani R., Friedman J.,"The elements of Statistical Learning. Data mining, Inference, and Prediction", Springer, New York - Berlin - Heidelberg 2001.
- Hiemstra Y. "Linear Regression Versus Backpropagation Networks to Predict Quarterly Stock Market Excess Returns", Computational Economics, pp. 67-76, 1996.
- Kohonen T.:"Self-organizing maps". Springer-Verlag, Berlin, 1995.
- Liu H., Motoda H.: "Feature Selection for Knowledge Discovery and Data Mining", Kluwer Academic Publishers, 1998.
- Lula P., Morajda J.: "Klasyfikacja wzorców występujących w finansowych szeregach czasowych przy użyciu sieci neuronowych Kohonena",. Zeszyty naukowe AE w Krakowie nr 604, Prace z zakresu informatyki i jej zastosowań, Kraków, 2002
- Morajda J., Domaradzki R.:"Application of cluster analysis performed by SOM neural network to the creation of financial transaction strategies", Journal of Applied Computer Science, 2005
- Morajda J.:"Applications of neural networks in the financial markets - selected="selected" aspects" - Proceedings of the 4thConference "Neural Networks and Their Applications" in Zakopane 18 22.05.1999, Częstochowa 1999.
- Morajda J.:"Neural networks as predictive models in financial futures trading" - Proceedings of the 5thConference "Neural Networks and Soft Computing" in Zakopane 6-10.06.2000, Częstochowa 2000.
- Morajda J.: "Neural Networks and Their Economic Applications" - w: "Artificial Intelligence and Security in Computing Systems" (eds: J. Sołdek, L. Drobiazgiewicz), Kluwer Academic Publishers, Boston/Dordrecht/London, 2003.
- Osowski S.: "Sieci neuronowe w ujęciu algorytmicznym", WNT, Warszawa, 1996.
- Refenes A.P. (ed.): "Neural networks in the capital markets", Wiley, Chichester, 1995.
- Schoeneburg E.:"Stock Price Prediction Using Neural Networks", A Project Report, Neurocomputing, vol.2, pp.17-27, 1990.
- Tadeusiewicz R. "Sieci neuronowe", Akademicka Oficyna Wydawnicza, Warszawa, 1993.
- Trippi R.R., Turban E.: "Neural Network in Finance and Investing", Probus Publishing, Chicago, 1996.
Referencje
[1] Minsky M., Papert S., "Perceptrons", MIT Press, Cambridge 1969 - Ta publikacja zahamowała rozwój sieci neuronowych na prawie 15 lat, gdyż zawierała formalny dowód na to, że jednowarstwowe sieci neuronowe mają bardzo ograniczony zakres zastosowań.
[2] Nawet jeśli krótka sprzedaż akcji (tzn. sprzedaż akcji pożyczonych od maklera, czyli zajęcie pozycji z ujemną liczbą akcji) w rzeczywistości nie jest na giełdzie możliwa, można ją zrealizować poprzez sprzedaż kontraktów terminowych na akcje (kontrakty terminowe na akcje KGHM są notowane na GPW w Warszawie). Posiadanie pozycji krótkiej (krótko sprzedanych akcji) jest zyskowne w przypadku spadku ich notowań.
[3] Nachylenie trendu było obliczone jako współczynnik kierunkowy prostej regresji dla pięciu ostatnich logarytmów notowań.
Niniejszy materiał, przygotowany przez DM BOŚ S.A. ma charakter wyłącznie informacyjny, prezentowany jest w celach edukacyjnych i nie stanowi porady prawnej oraz nie jest rekomendacją osobistą w ramach świadczenia usługi doradztwa inwestycyjnego zgodnie z przepisami prawa. DM BOŚ S.A. nie udziela gwarancji dokładności, aktualności, oraz kompletności niniejszych informacji. Zaleca się przeprowadzenie we własnym zakresie niezależnego przeglądu informacji z niniejszego materiału.



