Najbardziej charakterystyczną cechą Księżyca są jego fazy: pełnia, nów oraz kwadry, gdy terminator, czyli linia oddzielająca część oświetloną od nieoświetlonej, przebiega przez środek widocznej tarczy Księżyca. Odstęp czasu między kolejnymi nowiami Księżyca, równy 29 dniom 12 godzinom i 44 minutom (29,530589 dnia), zwany jest powszechnie miesiącem synodycznym lub lunacją. Miesiąc synodyczny jest o ponad 2 dni dłuższy od okresu obiegu Księżyca wokół Ziemi (po tym czasie Księżyc wraca do tego samego położenia względem gwiazd), zwanego także miesiącem syderycznym. Wynosi on 27 dni 7 godzin 43 minuty (27,321661 dnia) z powodu orbitalnego ruchu tej ostatniej dokoła Słońca (wzajemna konfiguracja tych trzech ciał: Słońca, Ziemi i Księżyca decyduje o tym, w jakiej fazie na ziemskim niebie świeci Księżyc)1 - rys. 1.
Rysunek 1. Różnica między długością miesiąca synodycznego a syderycznego

źródło: opracowanie własne
Istotne znaczenie przy konstrukcji kalendarza spiralnego pełni pierwiastek z kwadratowy z liczby Fibonacciego2 często oznaczanej jako F. Pierwiastek ilorazu kolejnych wyrazów ciągu Fibonacciego jest zbieżny do granicy równej3:
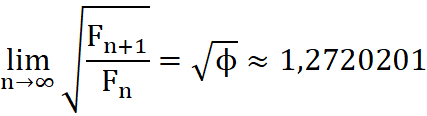
gdzie:
- Fn - oznacza n-ty wyraz ciągu Fibonacciego
Podstawowym narzędziem potrzebnym do analizy i stworzenia kalendarza spiralnego są dane historyczne. Ilość danych wejściowych określa precyzję otrzymywanej prognozy. Aby wykryć najważniejsze punkty zwrotne dla poszczególnych dekad, niezbędna jest analiza danych dziennych co najmniej z okresu 60 ostatnich lat. Jeśli dane takie są niedostępne, można zastosować dane z okresu od 20 do 25 lat. Analiza horyzontu dwu - lub trzyletniego pozwala na wykrycie krótkoterminowych zwrotów rynku, nie dostarcza jednak danych na temat punktów o największym znaczeniu.
Stworzenie kalendarza spiralnego składa się z kilku faz - rys.2:
- Wybór punktów zwrotnych - w naszym przykładzie oznaczonych przez D1 i D2.
- Rozwinięcia spiral czasowych4 z wybranych punktów zwrotnych i wyznaczenie dni docelowych - w naszym przykładzie oznaczonych jako D11 i D21
- Sprawdzenie warunków tzw. skupiska dat. Dla otrzymanych dni docelowych - w naszym przykładzie uzyskaliśmy jedno skupisko dat.
- Ustalenie ram czasowych dla dni docelowych i zaznaczenie okienek Carolana - w naszym przykładzie uzyskujemy dwie ramy czasowe i jedno okienko Carolana.
Rysunek 2. Etapy tworzenia kalendarza spiralnego na przykładzie dwu wybranych punktów zwrotnych D1 i D2. W rzeczywistości liczba punktów zwrotnych jest znacznie większa
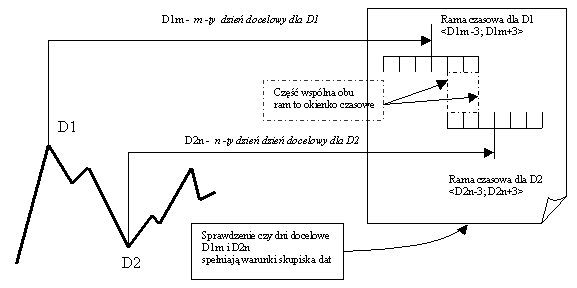
źródło: opracowanie własne
Ad1. Wybór punktów zwrotnych będących danymi wejściowymi dla dalszej analizy powinien być zdeterminowany ich istotnością na wykresie analizowanego aktywu. Ważne punkty z przeszłości będą tworzyć równie ważne punkty w przyszłości, jeśli łącząca je jednostka kalendarza będzie miała wysoką wartość indeksu. Słabsze ruchy rynku będą łączyć się z innymi słabszymi ruchami za pośrednictwem jednostek o niższych indeksach. Wybór przeszłych punktów dyktowany jest ilością dostępnych danych i charakterem zakładanej prognozy. Stosowanie tych zasad jest uzależnione od subiektywnych założeń analityka. Należy jednakże być świadomym, że dla małych indeksów jednostek kalendarza wybranie zbyt wielu punktów zwrotnych da w rezultacie ogromną ilość skupisk.
Ad2. Z każdego wybranego punktu zwrotnego rozwijamy spirale logarytmiczne odkładając na osi czasu odpowiednio odcinki równe: 29,5306*√Fn gdzie Fn jest kolejną liczbą ciągu Fibonacciego - tabela 1. W ten sposób na osi czasu otrzymujemy ciąg kolejnych dni docelowych Dn dla jednego punktu zwrotnego. W przypadku wybrania m punktów zwrotnych otrzymujemy ciąg dni docelowych Dmn gdzie m jest indeksem numerującym wybrane punkty zwrotne, a n indeksem numerującym kolejne liczby ciągu Fibonacciego (m i n należą do zbioru liczb naturalnych większych od zera).
Tabela 1. Kalendarz spiralny Carolana
1
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
1
1,00
29,53
2
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
1
1,00
29,53
3
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
2
1,41
41,8
4
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
3
1,73
51,1
5
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
5
2,24
66,0
6
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
8
2,83
83,5
7
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
13
3,61
106,5
8
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
21
4,58
135,3
9
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
34
5,83
172,2
10
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
55
7,42
219,0
11
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
89
9,43
278,6
12
Kolejna liczba
ciągu Fibonacciego
F
n
Liczba księżyców √Fn
Liczba dni 29,5306*√F
n
144
12,00
354,4
| Numer kolejny - indeks NA | Kolejna liczba ciągu Fibonacciego Fn |
Liczba księżyców √Fn |
Liczba dni 29,5306*√Fn |
|---|---|---|---|
| 1 | 1 | 1,00 | 29,53 |
| 2 | 1 | 1,00 | 29,53 |
| 3 | 2 | 1,41 | 41,8 |
| 4 | 3 | 1,73 | 51,1 |
| 5 | 5 | 2,24 | 66,0 |
| 6 | 8 | 2,83 | 83,5 |
| 7 | 13 | 3,61 | 106,5 |
| 8 | 21 | 4,58 | 135,3 |
| 9 | 34 | 5,83 | 172,2 |
| 10 | 55 | 7,42 | 219,0 |
| 11 | 89 | 9,43 | 278,6 |
| 12 | 144 | 12,00 | 354,4 |
źródło: Carolan C."Kalendarz spiralny", WIG - Press, Warszawa 1996
Liczba księżyców w tym kalendarzu wyrażana jest w pierwiastkach kwadratowych liczb ciągu Fibonacciego.
Ad3. Warunkiem koniecznym dla tego, aby dwa lub więcej dni docelowych stało się okienkiem Carolana, jest spełnianie przez nie warunku tzw. skupiska dat.
Skupisko dat jest to zbiór, co najmniej dwu położonych "blisko siebie" dat. Kalendarz spiralny składa się z dwu podciągów: o indeksach nieparzystych i indeksach parzystych. Prognozy o najwyższej jakości prognozy, powstają wtedy, gdy uzyskane daty należą do tego samego podciągu. Kolejną kwestią jest jeszcze "bliskość siebie" uzyskanych dat. Wg C. Carolana prognozowane daty uważa się za położone blisko siebie, jeśli generowane są przez jednostki tego samego ciągu, a różnica między nimi jest nie większa niż sześć dni kalendarzowych. W przypadku skupisk dat należących do różnych ciągów, jakość prognozy jest gorsza. W celu poprawienia jej wiarygodności zaostrzeniu ulegają stosowane w takim przypadku kryteria - różnica między datami należącymi do dwu podciągów, nie może przekroczyć trzech dni kalendarzowych.
Zbyt duża różnica indeksów jednostek kalendarza wpływa na niezgodność istotności prognozowanych jednostek.
Ostateczne parametry skupiska tzw. okienka Carolana przedstawiają się zatem następująco:
Tabela 2. Parametry skupiska wg C. Carolana
Różnica dni kalendarzowych
Ten sam ciąg
Różne ciągi
6 lub mniej dni
3 lub mniej
Różnica wartości indeksów
Ten sam ciąg
Różne ciągi
8 lub mniej
5 lub mniej
| Ten sam ciąg | Różne ciągi | |
|---|---|---|
| Różnica dni kalendarzowych | 6 lub mniej dni | 3 lub mniej |
| Różnica wartości indeksów | 8 lub mniej | 5 lub mniej |
źródło: Carolan C. "Kalendarz spiralny", WIG - Press, Warszawa 1996
Oczywiście może się zdarzyć, że utworzone okienka Carolana będą leżały bardzo blisko siebie. W takim przypadku mówimy o skupisku okienek.
Ad4. Każda otrzymana w skupisku data tworzy ramy czasowe, w obrębie których punkt zwrotny rynku, jeśli wystąpi, uznawany jest za precyzyjny. Punkty zwrotne występują najczęściej w centrum okienka, chociaż w rzeczywistości spotyka się także translacje lewo i prawostronne.
Carolan przyjmuje, że punkt zwrotny powinien wystąpić od 3 dni przed do 3 dni po dacie docelowej. W ten sposób każda data jest związana z siedmiodniowymi ramami tj. data ą trzy dni: <Dmn-3; Dmn+3>.
Ramy czasowe tworzą okienko czasowe, które jest częścią wspólną zachodzących na siebie ram czasowych powstałych z dwóch lub więcej dat danego skupiska. Punkt zwrotny rynku wystąpi zawsze w odległości nie większej niż 3 dni od każdej z prognozowanych dat.
Punkty zwrotne występują najczęściej w centrum okienka. Wśród zależności tworzonych przez jednostki kalendarza należące do tego samego ciągu najlepsze efekty daje formacja złotego podziału. Występuje ona, gdy różnica między indeksami jednostek jest równa dwa (iloraz=0,618) lub cztery (iloraz=0,3825). Jeśli dwa poprzednie punkty zwrotne tej formacji są tego samego typu (dna lub szczyty), istnieje wysokie prawdopodobieństwo wystąpienia kolejnego punktu tego właśnie typu. Rodzaj punktu jest trudny do określenia, jeśli poprzednie zwroty były różne lub gdy skupisko utworzone zostało przez jednostki różnych ciągów.
Z matematycznego punktu widzenia kalendarz spiralny jest transformacją do przestrzeni, w którym odległość od dowolnie wybranego punktu mierzona jest przy wykorzystaniu metryki6 ρ=29,5306*√Fn.
Strategia inwestowanie zgodnie z koncepcja zaproponowaną przez C. Carolana przewiduje 2 metody postępowania:
Agresywna strategia kupna i sprzedaży w trakcie trwania okna, gdy nie ma jeszcze pewności czy dane okienko zadziała. Jeśli okno sprawdzi się, to transakcja jest dokonana w punkcie zwrotnym lub blisko tego punktu, co pozwala uzyskać korzystniejsze ceny wejścia (wyjścia) na rynek.
Strategia zachowawcza, tj. zaczekanie do końca okienka i sprawdzenie czy okno zadziałało. Dopiero wtedy, tj. na samym brzegu okna, przeprowadzona zostaje określona transakcja. W przypadku tak zdefiniowanego sposobu postępowania do zawarcia transakcji nie dochodzi w samym punkcie zwrotnym - w związku z tym uzyskiwana stopa zwrotu będzie nieco mniejsza niż w przypadku posługiwania się strategią z punktu pierwszego. Eliminuje się w ten sposób wiele fałszywych sygnałów. Większe jest także prawdopodobieństwo odniesienia sukcesu i mniejsze ryzyko zawarcia transakcji.
Wprowadzenie do teorii R. Fischera
Metodę R. Fischera dobrze oddaje maksyma stanowiąca jedną z prawd poprawnego inwestowania: "Pamiętaj, że twoim celem jest grać dobrze, a nie grać często7".
Metoda Fischera stworzona została w 1983 r., kiedy to autor w trakcie seminariów na temat teorii Elliotta8 i liczb Fibonacciego zaproponował nową strategię inwestycyjną opartą o analizę czasu w kategoriach proporcji Fibonacciego9. W analizie nastawionej na wyznaczanie dni docelowych porządek fal stanowiący podstawowy element teorii Elliotta jest praktycznie bez znaczenia. Nie jest ważne czy mamy do czynienia z rynkiem zwyżkującym, zniżkującym czy też horyzontalnym.
Dzień docelowy (DD) w metodzie zaproponowanej przez R. Fischera10, obliczamy ze wzoru:
CI=B+(B-A)F lub CII=B+(B-A) o 1/Φ
Gdzie:
- A - data pierwszego dnia zwrotnego
- B - data drugiego dnia zwrotnego
- CI - data dnia docelowego (DD) dla podziału progresywnego - rys. 3
- CII - data dnia docelowego (DD) dla podziału degresywnego - rys. 4
Oba dni A i B są dniami zwrotnymi tego samego rzędu, tj. oba przypadają w lokalnych szczytach lub dnach. Dzień docelowy C może okazać się zarówno lokalnym szczytem jaki i lokalnym dnem. Poszczególne przypadki zostały przedstawione na rysunkach poniżej.
W praktyce mogą występować translacje dnia docelowego: do przodu lub w tył maksymalnie o 3 dni sesyjne (przyjęcie maksymalnej liczby dni translacji to oczywiście sprawa umowna - stanowi ona jeden ze stopni swobody tej metody). Tak, więc dzień docelowy należy do przedziału <DD-3, DD+3>. Kierunek i liczba dni translacji zależą w dużej mierze od siły rynku i długości trwającego trendu.
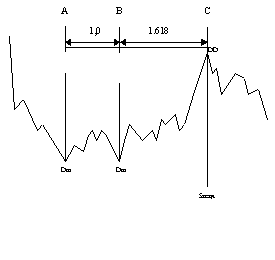
Rysunek 3. Wyznaczanie dnia docelowego na bazie odległości między punktami zwrotnymi A i B oraz współczynnika 1,618. Podział progresywny
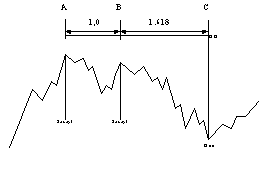
źródło: opracowanie własne
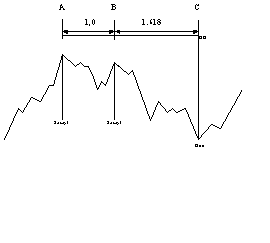
Rysunek 4. Przykład podziału degresywnego
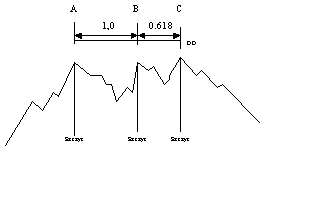
źródło: opracowanie własne
Rysunek 5. W dniu docelowym uzyskanym na bazie dwu szczytów może wystąpić lokalna górka
źródło: opracowanie własne
Rysunek 6. W dniu docelowym uzyskanym na bazie dwu szczytów może wystąpić lokalny dołek
źródło: opracowanie własne
Rysunek 7. W dniu docelowym uzyskanym na bazie dwu minimów może wystąpić lokalny dołek
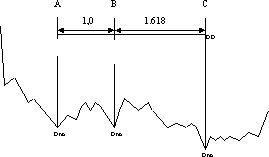
Źródło: opracowanie własne
Rysunek 8. W dniu docelowym uzyskanym na bazie dwu dołków może wystąpić lokalny szczyt
.gif)
źródło: opracowanie własne
Idealną będzie sytuacja, gdy dzień docelowy wyznaczony na podstawie dołków pokryje się z dniem docelowym wyznaczonym na podstawie szczytów. Przypadek taki należy do stosunkowo rzadkich. Najbardziej prawdopodobne jest to, że obie daty będą się różnić. Należy więc zadowolić się sytuacjami, w których dni docelowe znajdą się blisko siebie, tworząc wąski przedział czasowy (podobne do koncepcji okienka Carolana). Im więcej dni docelowych pojawia się w sąsiedztwie jakiegoś punktu, tym większe prawdopodobieństwo, że w tym właśnie miejscu nastąpi korekta lub całkowite odwrócenie trendu. Fischer dopuszcza stosowanie swojej metody na wykresach sporządzonych w układzie godzinowym, dziennym, tygodniowym czy miesięcznym11.
Dni docelowe wyliczone na podstawie danych dziennych są bardziej wiarygodne od dat wynikających z mniejszej skali czasowej, gdzie pojawia się bardzo dużo szumu12:
- Dzień docelowy może wystąpić przed szczytem bądź dołkiem lub się z nim pokrywać. Zdarza się to w sytuacji, gdy w dniu docelowym szczyt bądź dołek nie jest jeszcze widoczny
- Dzień docelowy może wypaść jeden dzień po szczycie lub dołku. Zdarza się, że dzień docelowy położony jest dalej niż faktyczny dołek lub szczyt, co może mieć istotny wpływ na wynik transakcji
- Dzień docelowy może wypaść więcej niż jeden dzień po szczycie lub dołku. W takim przypadku wskazana jest szczególna ostrożność przy zawieraniu transakcji
Autor metody zauważa, że jego metoda jest połączeniem koncepcji Elliotta i współczynników Fibonacciego, a dopiero kombinacja tych dwóch sposobów daje całościową metodę inwestycyjną. Sugeruje nawet, że ważniejsze od ustalania porządku fal, na którym koncentrował się R. Elliott, jest wykorzystanie proporcji Fibonacciego. Poza tym teoria fal powinna zostać uzupełniona o reguły zawierania transakcji13. Wg R. Fischera autor teorii fal - R. Elliott - napotykał trudności wynikające stąd, że liczby ciągu Fibonacciego są zbyt statyczne. Proponowanie przez R. Fischera wykorzystanie współczynników 0,618 i 1,618 w odniesieniu do szczytów i dołków jest podejściem zupełnie różnym od metody stosowanej w analizie czasu przez Elliotta, który wykorzystywał konkretne liczby (np. 3, 5, 8, ... tworząc metodę stref czasowych).
Rozszerzenie teorii Fischera można spotkać w książce E. Gately. Autor postuluje wykorzystanie dla projektowania przyszłych potencjalnych punktów zwrotnych następujących punktów14:
- Odcinka pomiędzy dwoma szczytami
- Odcinka pomiędzy dwoma dołkami
- Odcinka między dołkiem i szczytem lub szczytem i dołkiem
Punkt 1 i 2 metody E. Gately'a pokrywa się w pełni z tym, co zaproponował R. Fischer. Novum stanowi punkt trzeci. W programie Nature Pulse15 i Fibonacci Trader16 stworzono możliwość dynamicznego stosowania ciągu Fibonacciego tylko do oznaczonych tj. wybranych szczytów i dołków, co pozwala uzyskać przejrzysty obraz sytuacji, a jednocześnie zawiera czynnik subiektywny, uzależniający otrzymane wyniki od oceny analityka.
Użytkownik programu musi zaznaczyć punkty zwrotne, które mają być uwzględnione w analizie, po czym program odnosi liczby Fibonacciego do wszystkich możliwych kombinacji wygranych szczytów i dołków. Analiza przeprowadzana jest zarówno w pionie (analiza cenowa) i poziomie (analiza czasowa). Program wyświetla w pionie i poziomie liczbę wskazań danej ceny (tzn. liczbę linii Fibonacciego zgrupowanych na danym poziomie cenowym) i danego momentu czasowego.
Związek teorii Carolana z teorią Fischera
Koncepcja Carolana jest rozwinięciem koncepcji Fischera17. Dodanie do daty zmiany trendu jednostki z kalendarza spiralnego może być równoważne z konstrukcją złotego podziału odcinka. Dzieje się tak, gdy konstrukcja skupiska polega na wykorzystaniu liczb Fibonacciego różniących się o dwa indeksy (np. F20 i F22) wówczas konstrukcja Carolana prowadzi do "prawie" złotego podziału odcinka czasu:
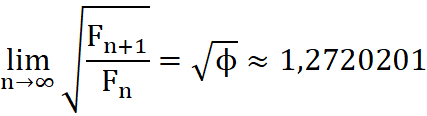
Teoria Carolana jest jednak ogólniejsza. Oś czasu nie musi być podzielona w sposób złoty czy prawie złoty. Możliwa jest konstrukcja okienek na podstawie liczb Fibonacciego różniących się niekoniecznie o 2 indeksy. Wówczas podział odcinka czasu nie jest złoty ani prawie złoty.
Skuteczność metody w wyznaczaniu punktów zwrotnych indeksu WIG
Na rys. 9 przedstawione zostały punkty zwrotne wykorzystane do konstrukcji kalendarza spiralnego Carolana w okresie od 16.04.1991 do 31.12.2002. Dla stworzenia kalendarza spiralnego na rok 2002 wykorzystane zostały punkty zwrotne z okresu 16.04.1991-31.12.2001.
W początkowym etapie rozwoju giełdy, tj. okresie kwiecień 1991 - maj 1993 r., punkty zwrotne nie są tak dobrze widoczne jak w późniejszych fazach ewolucji giełdy. Z uwagi na młody wiek polskiego rynku kapitałowego punkty zwrotne z początkowej fazy kwotowań powinny być zatem wybierane częściej niż w następnych stadiach.
Rysunek 9. Punkty zwrotne zostały wybrane dla konstrukcji kalendarza spiralnego
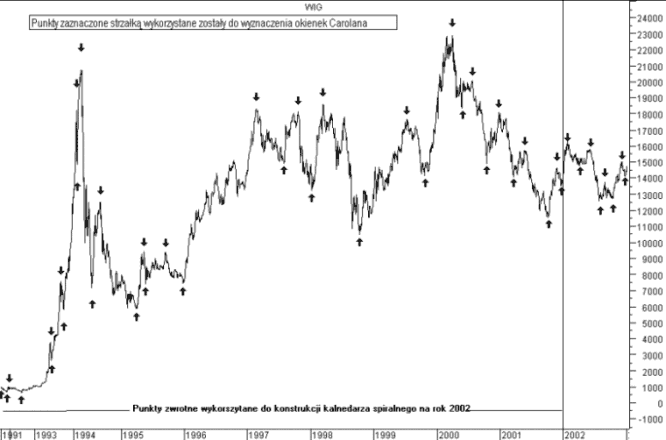
źródło: opracowanie własne
Strzałka skierowana do góry (w dół) oznacza lokalny dołek (szczyt) indeksu.
Punkty zwrotne występujące w trendzie spadkowym, mającym miejsce po dużej aprecjacji rynku, pełnią zdecydowanie ważniejszą rolę w przewidywaniu przyszłych dni docelowych niż punkty zwrotne z okresu hossy. W czasie bessy większego znaczenia nabiera oddziaływania pierwiastka psychologiczno - emocjonalnego. W związku z tym punkty zwrotne korekt występujących po hossach kończących się w marcu 1994, kwietniu 1995, lutym 1997 i marcu 2000 r., zostały wykorzystane nieco częściej.
C7
Na podstawie wybranych punktów otrzymujemy kalendarz spiralny. Tabela 3 ilustruje jego wybrany fragment. Poziomo na ciemnym tle zaznaczone zostały potencjalne dni docelowe (Ci/ci) będące rozwinięciem spirali, której ognisko położone jest w lokalnym minimum indeksu.
Na białym tle przedstawione zostały potencjalne dni docelowe (Ci/ci) będące rozwinięciem spirali, której ognisko położone jest w lokalnym maksimum indeksu.
C7
Tabela 3.1 Fragment kalendarza spiralnego C. Carolana dla wybranych punktów zwrotnych indeksu WIG
WIG
C1
C2
C3
C4
C5
DATA
29,5306
41,63815
51,08794
66,14854
83,5716
1000
C1
C2
C3
C4
C5
91.04.16
91.05.15
91.05.27
91.06.06
91.06.21
91.07.08
679
C1
C2
C3
C4
C5
91.10.01
91.10.30
91.11.11
91.11.21
91.12.06
91.12.23
1002
C1
C2
C3
C4
C5
91.12.10
92.01.08
92.01.20
92.01.30
92.02.14
92.03.02
635
C1
C2
C3
C4
C5
92.06.23
92.07.22
92.08.03
92.08.13
92.08.28
92.09.14
3784
C1
C2
C3
C4
C5
93.05.31
93.06.29
93.07.11
93.07.21
93.08.05
93.08.22
2638
C1
C2
C3
C4
C5
93.06.09
93.07.08
93.07.20
93.07.30
93.08.14
93.08.31
7561
C1
C2
C3
C4
C5
93.09.06
93.10.05
93.10.17
93.10.27
93.11.11
93.11.28
5848
C1
C2
C3
C4
C5
93.09.27
93.10.26
93.11.07
93.11.17
93.12.02
93.12.19
18218
C1
C2
C3
C4
C5
94.01.27
94.02.25
94.03.09
94.03.19
94.04.03
94.04.20
14871
C1
C2
C3
C4
C5
94.02.03
94.03.04
94.03.16
94.03.26
94.04.10
94.04.27
20760
C1
C2
C3
C4
C5
94.03.08
94.04.06
94.04.18
94.04.28
94.05.13
94.05.30
9980
C1
C2
C3
C4
C5
94.04.14
94.05.13
94.05.25
94.06.04
94.06.19
94.07.06
13557
C1
C2
C3
C4
C5
94.04.25
94.05.24
94.06.05
94.06.15
94.06.30
94.07.17
10399,7
C1
C2
C3
C4
C5
94.05.10
94.06.08
94.06.20
94.06.30
94.07.15
94.08.01
12479
C1
C2
C3
C4
C5
94.05.24
94.06.22
94.07.04
94.07.14
94.07.29
94.08.15
7215
C1
C2
C3
C4
C5
94.06.23
94.07.22
94.08.03
94.08.13
94.08.28
94.09.14
12507
C1
C2
C3
C4
C5
94.08.23
94.09.21
94.10.03
94.10.13
94.10.28
94.11.14
6716
C1
C2
C3
C4
C5
94.11.16
94.12.15
94.12.27
95.01.06
95.01.21
95.02.07
8177
C1
C2
C3
C4
C5
94.12.01
94.12.30
95.01.11
95.01.21
95.02.05
95.02.22
5926
C1
C2
C3
C4
C5
95.02.03
95.03.04
95.03.16
95.03.26
95.04.10
95.04.27
6903
C1
C2
C3
C4
C5
95.02.24
95.03.25
95.04.06
95.04.16
95.05.01
95.05.18
5904
C1
C2
C3
C4
C5
95.03.28
95.04.26
95.05.08
95.05.18
95.06.02
95.06.19
9396
C1
C2
C3
C4
C5
95.05.12
95.06.10
95.06.22
95.07.02
95.07.17
95.08.03
| DNO | C1 | C2 | C3 | C4 | C5 | |
|---|---|---|---|---|---|---|
| WIG | DATA | 29,5306 | 41,63815 | 51,08794 | 66,14854 | 83,5716 |
| 1000 | 91.04.16 | 91.05.15 | 91.05.27 | 91.06.06 | 91.06.21 | 91.07.08 |
| 679 | 91.10.01 | 91.10.30 | 91.11.11 | 91.11.21 | 91.12.06 | 91.12.23 |
| 1002 | 91.12.10 | 92.01.08 | 92.01.20 | 92.01.30 | 92.02.14 | 92.03.02 |
| 635 | 92.06.23 | 92.07.22 | 92.08.03 | 92.08.13 | 92.08.28 | 92.09.14 |
| 3784 | 93.05.31 | 93.06.29 | 93.07.11 | 93.07.21 | 93.08.05 | 93.08.22 |
| 2638 | 93.06.09 | 93.07.08 | 93.07.20 | 93.07.30 | 93.08.14 | 93.08.31 |
| 7561 | 93.09.06 | 93.10.05 | 93.10.17 | 93.10.27 | 93.11.11 | 93.11.28 |
| 5848 | 93.09.27 | 93.10.26 | 93.11.07 | 93.11.17 | 93.12.02 | 93.12.19 |
| 18218 | 94.01.27 | 94.02.25 | 94.03.09 | 94.03.19 | 94.04.03 | 94.04.20 |
| 14871 | 94.02.03 | 94.03.04 | 94.03.16 | 94.03.26 | 94.04.10 | 94.04.27 |
| 20760 | 94.03.08 | 94.04.06 | 94.04.18 | 94.04.28 | 94.05.13 | 94.05.30 |
| 9980 | 94.04.14 | 94.05.13 | 94.05.25 | 94.06.04 | 94.06.19 | 94.07.06 |
| 13557 | 94.04.25 | 94.05.24 | 94.06.05 | 94.06.15 | 94.06.30 | 94.07.17 |
| 10399,7 | 94.05.10 | 94.06.08 | 94.06.20 | 94.06.30 | 94.07.15 | 94.08.01 |
| 12479 | 94.05.24 | 94.06.22 | 94.07.04 | 94.07.14 | 94.07.29 | 94.08.15 |
| 7215 | 94.06.23 | 94.07.22 | 94.08.03 | 94.08.13 | 94.08.28 | 94.09.14 |
| 12507 | 94.08.23 | 94.09.21 | 94.10.03 | 94.10.13 | 94.10.28 | 94.11.14 |
| 6716 | 94.11.16 | 94.12.15 | 94.12.27 | 95.01.06 | 95.01.21 | 95.02.07 |
| 8177 | 94.12.01 | 94.12.30 | 95.01.11 | 95.01.21 | 95.02.05 | 95.02.22 |
| 5926 | 95.02.03 | 95.03.04 | 95.03.16 | 95.03.26 | 95.04.10 | 95.04.27 |
| 6903 | 95.02.24 | 95.03.25 | 95.04.06 | 95.04.16 | 95.05.01 | 95.05.18 |
| 5904 | 95.03.28 | 95.04.26 | 95.05.08 | 95.05.18 | 95.06.02 | 95.06.19 |
| 9396 | 95.05.12 | 95.06.10 | 95.06.22 | 95.07.02 | 95.07.17 | 95.08.03 |
Tabela 3.2 Fragment kalendarza spiralnego C. Carolana dla wybranych punktów zwrotnych indeksu WIG
WIG
C6
C7
C8
C9
C10
DATA
106,6055
135,2501
172,1634
219,1171
278,4736
1000
C6
C7
C8
C9
C10
91.04.16
91.07.31
91.08.29
91.10.05
91.11.21
92.01.19
679
C6
C7
C8
C9
C10
91.10.01
92.01.15
92.02.13
92.03.21
92.05.07
92.07.05
1002
C6
C7
C8
C9
C10
91.12.10
92.03.25
92.04.23
92.05.30
92.07.16
92.09.13
635
C6
C7
C8
C9
C10
92.06.23
92.10.07
92.11.05
92.12.12
93.01.28
93.03.28
3784
C6
C7
C8
C9
C10
93.05.31
93.09.14
93.10.13
93.11.19
94.01.05
94.03.05
2638
C6
C7
C8
C9
C10
93.06.09
93.09.23
93.10.22
93.11.28
94.01.14
94.03.14
7561
C6
C7
C8
C9
C10
93.09.06
93.12.21
94.01.19
94.02.25
94.04.13
94.06.11
5848
C6
C7
C8
C9
C10
93.09.27
94.01.11
94.02.09
94.03.18
94.05.04
94.07.02
18218
C6
C7
C8
C9
C10
94.01.27
94.05.13
94.06.11
94.07.18
94.09.03
94.11.01
14871
C6
C7
C8
C9
C10
94.02.03
94.05.20
94.06.18
94.07.25
94.09.10
94.11.08
20760
C6
C7
C8
C9
C10
94.03.08
94.06.22
94.07.21
94.08.27
94.10.13
94.12.11
9980
C6
C7
C8
C9
C10
94.04.14
94.07.29
94.08.27
94.10.03
94.11.19
95.01.17
13557
C6
C7
C8
C9
C10
94.04.25
94.08.09
94.09.07
94.10.14
94.11.30
95.01.28
10399,7
C6
C7
C8
C9
C10
94.05.10
94.08.24
94.09.22
94.10.29
94.12.15
95.02.12
12479
C6
C7
C8
C9
C10
94.05.24
94.09.07
94.10.06
94.11.12
94.12.29
95.02.26
7215
C6
C7
C8
C9
C10
94.06.23
94.10.07
94.11.05
94.12.12
95.01.28
95.03.28
12507
C6
C7
C8
C9
C10
94.08.23
94.12.07
95.01.05
95.02.11
95.03.30
95.05.28
6716
C6
C7
C8
C9
C10
94.11.16
95.03.02
95.03.31
95.05.07
95.06.23
95.08.21
8177
C6
C7
C8
C9
C10
94.12.01
95.03.17
95.04.15
95.05.22
95.07.08
95.09.05
5926
C6
C7
C8
C9
C10
95.02.03
95.05.20
95.06.18
95.07.25
95.09.10
95.11.08
6903
C6
C7
C8
C9
C10
95.02.24
95.06.10
95.07.09
95.08.15
95.10.01
95.11.29
5904
C6
C7
C8
C9
C10
95.03.28
95.07.12
95.08.10
95.09.16
95.11.02
95.12.31
9396
C6
C7
C8
C9
C10
95.05.12
95.08.26
95.09.24
95.10.31
95.12.17
96.02.14
| DNO | C6 | C7 | C8 | C9 | C10 | |
|---|---|---|---|---|---|---|
| WIG | DATA | 106,6055 | 135,2501 | 172,1634 | 219,1171 | 278,4736 |
| 1000 | 91.04.16 | 91.07.31 | 91.08.29 | 91.10.05 | 91.11.21 | 92.01.19 |
| 679 | 91.10.01 | 92.01.15 | 92.02.13 | 92.03.21 | 92.05.07 | 92.07.05 |
| 1002 | 91.12.10 | 92.03.25 | 92.04.23 | 92.05.30 | 92.07.16 | 92.09.13 |
| 635 | 92.06.23 | 92.10.07 | 92.11.05 | 92.12.12 | 93.01.28 | 93.03.28 |
| 3784 | 93.05.31 | 93.09.14 | 93.10.13 | 93.11.19 | 94.01.05 | 94.03.05 |
| 2638 | 93.06.09 | 93.09.23 | 93.10.22 | 93.11.28 | 94.01.14 | 94.03.14 |
| 7561 | 93.09.06 | 93.12.21 | 94.01.19 | 94.02.25 | 94.04.13 | 94.06.11 |
| 5848 | 93.09.27 | 94.01.11 | 94.02.09 | 94.03.18 | 94.05.04 | 94.07.02 |
| 18218 | 94.01.27 | 94.05.13 | 94.06.11 | 94.07.18 | 94.09.03 | 94.11.01 |
| 14871 | 94.02.03 | 94.05.20 | 94.06.18 | 94.07.25 | 94.09.10 | 94.11.08 |
| 20760 | 94.03.08 | 94.06.22 | 94.07.21 | 94.08.27 | 94.10.13 | 94.12.11 |
| 9980 | 94.04.14 | 94.07.29 | 94.08.27 | 94.10.03 | 94.11.19 | 95.01.17 |
| 13557 | 94.04.25 | 94.08.09 | 94.09.07 | 94.10.14 | 94.11.30 | 95.01.28 |
| 10399,7 | 94.05.10 | 94.08.24 | 94.09.22 | 94.10.29 | 94.12.15 | 95.02.12 |
| 12479 | 94.05.24 | 94.09.07 | 94.10.06 | 94.11.12 | 94.12.29 | 95.02.26 |
| 7215 | 94.06.23 | 94.10.07 | 94.11.05 | 94.12.12 | 95.01.28 | 95.03.28 |
| 12507 | 94.08.23 | 94.12.07 | 95.01.05 | 95.02.11 | 95.03.30 | 95.05.28 |
| 6716 | 94.11.16 | 95.03.02 | 95.03.31 | 95.05.07 | 95.06.23 | 95.08.21 |
| 8177 | 94.12.01 | 95.03.17 | 95.04.15 | 95.05.22 | 95.07.08 | 95.09.05 |
| 5926 | 95.02.03 | 95.05.20 | 95.06.18 | 95.07.25 | 95.09.10 | 95.11.08 |
| 6903 | 95.02.24 | 95.06.10 | 95.07.09 | 95.08.15 | 95.10.01 | 95.11.29 |
| 5904 | 95.03.28 | 95.07.12 | 95.08.10 | 95.09.16 | 95.11.02 | 95.12.31 |
| 9396 | 95.05.12 | 95.08.26 | 95.09.24 | 95.10.31 | 95.12.17 | 96.02.14 |
źródło: opracowanie własne
Na podstawie kalendarza spiralnego konstruujemy okienka Carolana na rok 2002 i 2003 Tabele 4 i 5. Okienka oznaczone zostały kolorem szarym.
Przy konstrukcji kalendarza zostały przyjęte następujące oznaczenia:
- c - mała litera c oznacza sygnał pochodzący z lokalnego dołka indeksu giełdowego WIG
- C - duża litera c oznacza sygnał pochodzący z lokalnej górki indeksu giełdowego WIG
- indeks - liczba przy małej lub dużej literze c oznacza numer kolejnej liczby w ciągu Fibonacciego.
C7
Części wspólne skupisk okienek Carolana zostały oznaczone poprzez obramowanie czarną obwódką komórek wspólnych.
I tak np. C8 - oznacza sygnał pochodzący z lokalnej górki, odpowiadający ósmemu wyrazowi ciągu Fibonacciego tj. 172,16 dniom liczonych od tego właśnie szczytu.
Literą F w kalendarzu zaznaczone zostały sygnały Fischera omówione w dalszej części artykułu.
Tabela 4.1 Otrzymane sygnały Carolana i Fischera w 2002 roku
1
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
c16
-
-
-
-
-
2
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
C7
c15
-
3
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
C19
c11
-
-
-
4
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
5
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
C6
-
-
-
6
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
c12
-
-
-
-
-
7
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
c12
8
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
C19
-
9
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
C3
-
-
-
c13, c9
-
10
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
C5
-
-
C8
-
11
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
C11
-
12
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
C18
-
13
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
c20
-
-
-
14
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
c19
c7
C13, C12
-
-
-
15
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
16
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
c6
-
-
-
-
-
17
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
18
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
C21
-
-
-
-
-
19
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
20
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
C20
-
C17
-
-
21
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
c17
-
-
-
-
22
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
23
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
c8
-
-
-
24
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
C15, C4
C10
-
-
-
-
25
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
c14
-
26
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
F
-
C14
-
-
C9
27
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
28
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
29
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
30
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
31
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
| Dzień | Styczeń | Luty | Marzec | Kwiecień | Maj | Czerwiec |
|---|---|---|---|---|---|---|
| 1 | c16 | - | - | - | - | - |
| 2 | - | - | - | C7 | c15 | - |
| 3 | C19 | c11 | - | - | - | |
| 4 | - | - | - | - | - | - |
| 5 | - | - | C6 | - | - | - |
| 6 | c12 | - | - | - | - | - |
| 7 | - | - | - | - | - | c12 |
| 8 | - | - | - | - | C19 | - |
| 9 | C3 | - | - | - | c13, c9 | - |
| 10 | - | C5 | - | - | C8 | - |
| 11 | - | - | - | - | C11 | - |
| 12 | - | - | - | - | C18 | - |
| 13 | - | - | c20 | - | - | - |
| 14 | c19 | c7 | C13, C12 | - | - | - |
| 15 | - | - | - | - | - | - |
| 16 | c6 | - | - | - | - | - |
| 17 | - | - | - | - | - | - |
| 18 | C21 | - | - | - | - | - |
| 19 | - | - | - | - | - | - |
| 20 | - | C20 | - | C17 | - | - |
| 21 | - | c17 | - | - | - | - |
| 22 | - | - | - | - | - | - |
| 23 | - | - | c8 | - | - | - |
| 24 | C15, C4 | C10 | - | - | - | - |
| 25 | - | - | - | - | c14 | - |
| 26 | F | - | C14 | - | - | C9 |
| 27 | - | - | - | - | - | - |
| 28 | - | - | - | - | - | - |
| 29 | - | - | - | - | - | - |
| 30 | - | - | - | - | - | - |
| 31 | - | - | - | - | - | - |
Tabela 4.2 Otrzymane sygnały Carolana i Fischera w 2002 roku
1
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
2
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
3
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
F
-
-
-
4
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
C16
-
-
5
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
c21
-
-
-
-
-
6
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
7
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
c10
-
-
-
-
c20
8
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
c13
C11
-
9
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
c15
10
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
C15
-
-
11
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
12
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
c14
-
-
13
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
C20
c19
C21
-
-
-
14
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
15
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
C13
c12
-
-
-
-
16
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
C13
17
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
18
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
c17
C14
19
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
20
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
c20, C14
-
-
c18
-
-
21
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
F
c11
-
-
-
22
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
C20
-
-
-
-
23
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
24
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
C10
-
-
-
-
25
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
26
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
c12
27
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
28
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
29
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
30
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
31
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
| Dzień | Lipiec | Sierpień | Wrzesień | Październik | Listopad | Grudzień |
|---|---|---|---|---|---|---|
| 1 | - | - | - | - | - | - |
| 2 | - | - | - | - | - | - |
| 3 | - | - | F | - | - | - |
| 4 | - | - | - | C16 | - | - |
| 5 | c21 | - | - | - | - | - |
| 6 | - | - | - | - | - | - |
| 7 | c10 | - | - | - | - | c20 |
| 8 | - | - | - | c13 | C11 | - |
| 9 | - | - | - | - | - | c15 |
| 10 | - | - | - | C15 | - | - |
| 11 | - | - | - | - | - | - |
| 12 | - | - | - | c14 | - | - |
| 13 | C20 | c19 | C21 | - | - | - |
| 14 | - | - | - | - | - | - |
| 15 | C13 | c12 | - | - | - | - |
| 16 | - | - | - | - | - | C13 |
| 17 | - | - | - | - | - | - |
| 18 | - | - | - | - | c17 | C14 |
| 19 | - | - | - | - | - | - |
| 20 | c20, C14 | - | - | c18 | - | - |
| 21 | - | F | c11 | - | - | - |
| 22 | - | C20 | - | - | - | - |
| 23 | - | - | - | - | - | - |
| 24 | - | C10 | - | - | - | - |
| 25 | - | - | - | - | - | - |
| 26 | - | - | - | - | - | c12 |
| 27 | - | - | - | - | - | - |
| 28 | - | - | - | - | - | - |
| 29 | - | - | - | - | - | - |
| 30 | - | - | - | - | - | - |
| 31 | - | - | - | - | - | - |
źródło: opracowanie własne
Powstałe okienka i wybrane dni docelowe naniesione zostały na wykres indeksu WIG w celu weryfikacji skuteczności otrzymywanych na ich podstawie sygnałów. Okienka zaznaczone zostały przy pomocy prostokątów, których szerokość podstawy odpowiada długości czasu trwania uzyskanego okienka Carolana. Na wykresie umieszczone zostały też te dni docelowe, które nie tworzą okienek Carolana, ale wyznaczają potencjalny lokalny punkt zwrotny rynku oraz sygnały Fischera - rys. 10.
Rysunek 10. Okienka Carolana i sygnały Fischera w 2002 roku
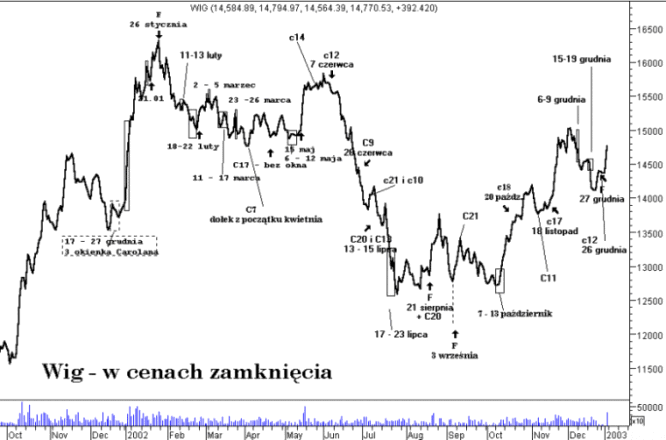
źródło: opracowanie własne
W 2002 r. najważniejszymi wskazaniami punktów zwrotnych indeksu Wig były okienka Carolana w następujących okresach czasu:
- początek stycznia - wybicie indeksu w górę. Okno styczniowe stanowiło potwierdzenie okna z końca grudnia 2001 sygnalizującego lokalne minimum indeksu.
- połowa lutego - punkt zwrotny sygnalizujący nadchodzącą korektę techniczną
- koniec lutego - koniec korekty spadkowej
- początek marca - wskazanie lokalnego szczytu indeksu
- połowa marca - wskazanie nadchodzącej fali spadkowej indeksu
- początek maja - sygnalizacja lokalnego minimum indeksu
- koniec lipca - zakończenie silnej fali spadkowej i początek formacji bazy
- początek października - początek jesiennej zwyżki indeksu
- początek grudnia - koniec jesiennej aprecjacji indeksu i początek korekty notowań.
- połowa grudnia - wskazanie jeszcze jednej fali spadkowej indeksu
W analizowanym okresie czasu najważniejszymi wskazaniami lokalnych punktów zwrotnych przez pojedyncze sygnały Ci, nie tworzącymi okienek Carolana były:
- sygnały C15 i C4 z 24 stycznia - wskazanie lokalnego szczytu indeksu w dniu 25 stycznia
- sygnał C7 z 2 kwietnia - wskazanie lokalnego dołka indeksu z 3 kwietnia
- sygnał C17 z 20 kwietnia - wskazanie lokalnego dołka indeksu z 19 kwietnia
- sygnał c14 z 25 maja - wskazanie lokalnego maksimum indeksu z dnia 3 czerwca. Należy pokreślić jednak fakt, że ekstremum indeksu w dniu 3 czerwca było fałszywym wybiciem. Kształtowanie przez indeks formacji wierzchołkowej trwało od 17 maja do 3 czerwca.
- sygnał c12 z 7 czerwca - wskazanie lokalnego maksimum indeksu z dnia 3 czerwca. Sygnał c12 wraz ze wskazaniem c14 z dnia 25 maja stanowiły bardzo poważne ostrzeżenie przed nadchodzą korektą notowań. W tym przypadku możne wręcz mówić o efekcie synergii obu wskazań.
- sygnał C9 z 26 czerwca - wskazanie lokalnej korekty technicznej indeksu w silnym trendzie spadkowym
- sygnały c21 i c10 odpowiednio z 5 i 7 lipca - wskazanie lokalnej korekty technicznej indeksu w silnym trendzie spadkowym
- sygnały C20 i C13 odpowiednio z 13 i 15 lipca - wskazanie lokalnej korekty technicznej indeksu w silnym trendzie spadkowym indeksu
- sygnał C20 z 22 sierpnia - wskazanie (wraz z sygnałem Fischera) lokalnego minimum indeksu
- sygnał C21 z 13 września - wskazanie lokalnego szczytu indeksu z dnia 11 września
- sygnał c18 z 20 października - wskazanie końca pierwszej fali wzrostowej z jesiennej zwyżki notowań
- sygnał C11 z 8 listopada - wskazanie lokalnego dna stanowiącego zakończenie fali korekty. Indeks osiągnął swoje minimum w dniu 7 listopada.
- sygnał c17 z 18 listopada - początek nowej fali wzrostowej
- sygnał c12 z 26 grudnia - sygnalizacja nowej fali zwyżki indeksu.
Do wyznaczenia potencjalnych punktów zwrotnych za pomocą metody Fischera w 2002 r. wykorzystane zostały ekstrema z metody Carolana przypadające w okresie 16.04.1991 - 31.12.2001. Otrzymane w ten sposób wskazania na rok 2002 przedstawione zostały w tabeli nr 5. Dzień potencjalnej zmiany tendencji obliczony z wykorzystaniem metody Fischera zaznaczony został przy pomocy litery F. W 2002 r. wystąpiły 3 sygnały Fischera:
- W dniu 26 stycznia - wskazanie to sygnalizowało szczyt indeksu Wig, który wystąpił w dniu 25 stycznia.
- W dniu 21 sierpnia - wskazanie lokalnego dołka indeksu z dnia 20 sierpnia
- W dniu 3 września - wskazanie lokalnego dołka indeksu z dnia 5 września
Czwarty sygnał Fischera możemy uzyskać biorąc pod uwagę następujące ekstrema lokalne indeksu: szczyt z 25 stycznia i szczyt z 3 czerwca 2002 r. Sygnał wypadł w dniu 27 grudnia i sygnalizował lokalne dno indeksu poprzedzające styczniową falę hossy.
Warto podkreślić fakt, że potwierdzenie sygnału Fischera przez sygnał Carolana nie tworzący okna i leżący w pobliżu daty wyznaczonej przez metodę Fischera, stanowi element znacznie zwiększający prawdopodobieństwo wystąpienia punktu zwrotnego w pobliżu daty sygnału Fischera. Taki przypadek miał miejsce dla sygnałów: styczniowego, sierpniowego i grudniowego.
Tabela 5.1 Kalendarz Carolana i sygnały Fischera na rok 2003
1
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
c9
-
-
-
2
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
C18, C10
3
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
C15
-
-
-
-
4
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
C9
F. c7
-
5
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
c18, c6
-
-
6
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
C20, C4
-
-
-
-
7
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
C18, c10
-
-
-
-
-
8
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
C9
-
c12, C10
-
-
-
9
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
c3
-
-
-
-
10
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
c16, C7
-
-
-
-
c8
11
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
12
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
C2
C12
-
-
-
-
13
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
c8, F
-
c14, c5
-
-
-
14
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
C11
c7
-
C7
c9
C13
15
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
16
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
C8
-
-
-
-
17
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
18
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
c1
-
C6
F
-
-
19
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
20
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
C12
-
C16
21
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
c6
-
-
-
C14
-
22
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
C3, F
-
-
-
-
-
23
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
C5
-
-
C11, C8
-
24
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
c4
c11
-
-
-
25
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
26
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
27
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
-
-
-
28
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
c21, c8
c15, c13
-
c12
29
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
-
-
-
c10
-
-
30
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
c2
-
-
-
-
-
31
Styczeń
Luty
Marzec
Kwiecień
Maj
Czerwiec
F
-
-
-
-
-
| Dzień | Styczeń | Luty | Marzec | Kwiecień | Maj | Czerwiec |
|---|---|---|---|---|---|---|
| 1 | - | - | c9 | - | - | - |
| 2 | - | - | - | - | - | C18, C10 |
| 3 | - | C15 | - | - | - | - |
| 4 | - | - | - | C9 | F. c7 | - |
| 5 | - | - | - | c18, c6 | - | - |
| 6 | - | C20, C4 | - | - | - | - |
| 7 | C18, c10 | - | - | - | - | - |
| 8 | C9 | - | c12, C10 | - | - | - |
| 9 | - | c3 | - | - | - | - |
| 10 | c16, C7 | - | - | - | - | c8 |
| 11 | - | - | - | - | - | - |
| 12 | C2 | C12 | - | - | - | - |
| 13 | c8, F | - | c14, c5 | - | - | - |
| 14 | C11 | c7 | - | C7 | c9 | C13 |
| 15 | - | - | - | - | - | - |
| 16 | - | C8 | - | - | - | - |
| 17 | - | - | - | - | - | - |
| 18 | c1 | - | C6 | F | - | - |
| 19 | - | - | - | - | - | - |
| 20 | - | - | - | C12 | - | C16 |
| 21 | c6 | - | - | - | C14 | - |
| 22 | C3, F | - | - | - | - | - |
| 23 | - | C5 | - | - | C11, C8 | - |
| 24 | - | c4 | c11 | - | - | - |
| 25 | - | - | - | - | - | - |
| 26 | - | - | - | - | - | - |
| 27 | - | - | - | - | - | - |
| 28 | - | - | c21, c8 | c15, c13 | - | c12 |
| 29 | - | - | - | c10 | - | - |
| 30 | c2 | - | - | - | - | - |
| 31 | F | - | - | - | - | - |
Tabela 5.2 Kalendarz Carolana i sygnały Fischera na rok 2003
1
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
c14
-
-
2
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
3
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
4
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
C15
-
-
-
-
-
5
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
C15
6
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
C10
-
c20
-
7
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
c13
-
-
-
-
-
8
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
9
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
C9
-
-
-
-
c11
10
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
11
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
c20
-
-
-
12
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
c10
-
-
-
-
-
13
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
C19
-
c14
14
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
c11
-
-
C16
-
-
15
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
16
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
17
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
C12
F
-
C14
-
18
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
c12
-
-
19
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
F
c16
-
-
-
-
20
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
21
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
C17, C13
-
-
C13, C11
-
22
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
23
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
24
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
c10
-
-
-
25
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
26
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
c11
C20
-
-
27
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
c9
C12
c15
-
c17
-
28
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
C13
29
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
c13
-
-
30
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
-
31
Lipiec
Sierpień
Wrzesień
Październik
Listopad
Grudzień
-
-
-
-
-
c18, c12
| Dzień | Lipiec | Sierpień | Wrzesień | Październik | Listopad | Grudzień |
|---|---|---|---|---|---|---|
| 1 | - | - | - | c14 | - | - |
| 2 | - | - | - | - | - | - |
| 3 | - | - | - | - | - | - |
| 4 | C15 | - | - | - | - | - |
| 5 | - | - | - | - | - | C15 |
| 6 | - | - | C10 | - | c20 | - |
| 7 | c13 | - | - | - | - | - |
| 8 | - | - | - | - | - | - |
| 9 | C9 | - | - | - | - | c11 |
| 10 | - | - | - | - | - | - |
| 11 | - | - | c20 | - | - | - |
| 12 | c10 | - | - | - | - | - |
| 13 | - | - | - | C19 | - | c14 |
| 14 | c11 | - | - | C16 | - | - |
| 15 | - | - | - | - | - | - |
| 16 | - | - | - | - | - | - |
| 17 | - | C12 | F | - | C14 | - |
| 18 | - | - | - | c12 | - | - |
| 19 | F | c16 | - | - | - | - |
| 20 | - | - | - | - | - | - |
| 21 | - | C17, C13 | - | - | C13, C11 | - |
| 22 | - | - | - | - | - | - |
| 23 | - | - | - | - | - | - |
| 24 | - | - | c10 | - | - | - |
| 25 | - | - | - | - | - | - |
| 26 | - | - | c11 | C20 | - | - |
| 27 | c9 | C12 | c15 | - | c17 | - |
| 28 | - | - | - | - | - | C13 |
| 29 | - | - | - | c13 | - | - |
| 30 | - | - | - | - | - | - |
| 31 | - | - | - | - | - | c18, c12 |
źródło: opracowanie własne
Wykorzystując punkty zwrotne indeksu Wig zaznaczone na rys. 10 otrzymujemy kalendarz Carolana i sygnały Fischera na rok 2003 - tabela nr 5.
W miesiącu styczniu występują dwa przedziały czasowe (zaznaczone kolorem szarym), w których może dojść do zmiany tendencji giełdowej. Pierwszy od 4 do 16 stycznia jest skupiskiem kilku okienek czasowych o różnej sile. Występowanie sygnałów o dużych wartościach indeksów: c16 i C18 potwierdzonych wskazaniem Fischera, znacznie zwiększa prawdopodobieństwo wystąpienia punktu zwrotnego (lub punktów zwrotnych). W tak szerokim oknie często dochodzi do powstania dwu niezależnych wskazań np. w dniu 7 i 13 stycznia, w których koncentrują się części wspólne poszczególnych okien składowych skupiska.
Drugie okno: 19 - 24 jest co prawda także uzupełnione wskazaniem Fischera, zwiększającym szansę na zmianę tendencji giełdowej, jednak niska wartość indeksów sygnałów tworzących okienko nieco osłabią tę szansę.
Na początku miesiąca lutego zauważamy dwa okna tworzące skupisko ze wspólną częścią wypadającą w dniu 6 lutego. Skupisko okien: 11 - 17 lutego jest już nieco słabsze w porównaniu ze styczniowym i poprzednim. Ostatnie lutowe okno z uwagi na bardzo niską wartość indeksów je tworzących, wydaje się posiadać mały ciężar gatunkowy.
Występujące w pierwszej połowie marca skupisko okien utworzonych z sygnałów o dużych wartościach indeksów, sugeruje powstanie potencjalnego sygnału zwrotnego indeksu w dniach 10 -11 marca. Drugie okno marcowe nie jest już tak silne.
Wystąpienie sygnału zwrotnego indeksu w drugim z kwietniowych okien (skupisko trzech okienek Carolana) wydaje się być znacznie bardziej prawdopodobne niż w pierwszym.
W miesiącu maju powstało jedno silne skupisko okien 20 -24 maja.
W miesiącu czerwcu sytuacja przedstawia się wręcz odwrotnie do tego, co obserwujemy w kwietniu - przemawia za tym duża wartości indeksów tworzących pierwsze okno Carolana w stosunku do indeksów okna drugiego.
W miesiącu lipcu zauważamy dwa skupiska okien z częściami wspólnymi w dniach: 6 -7 i 11 lipca. W ósmym miesiącu roku powstało skupisko okien z częścią wspólną w dniach 18 - 20. Dużą wartość indeksów sygnałów tworzących to okienko znacznie zwiększa jego wagę. W trzech następnych miesiącach powstało po jednym skupisku okienek Carolana z częściami wspólnymi w dniach: 24 - 27 września, 17 października i 24 listopada. Z dwu okien grudniowych, biorąc pod uwagę wartość indeksów sygnałów Carolana je tworzących, zdecydowanie silniejszym jest okno drugie.
W roku 2003 utworzonych zostało łącznie 7 sygnałów Fischera, z czego aż 5 przypada w pierwszej połowie roku. Cztery z nich potwierdzone zostały niezależnie przez sygnały Carolana (dwa sygnały Fischera występują nawet w okienku Carolana) - fakt ten dodatkowo zwiększa ich wagę.
W literaturze ocenia się skuteczność metody Carolana na 60 - 70%18. Efektywne stosowanie kalendarza spiralnego na rynku amerykańskim daje zwykle od 0 do 3 sygnałów w miesiącu19.
System transakcyjny oparty na sygnałach Fischera i okienkach Carolana
Z uwagi na fakt, że okienka Carolana nie wyznaczają wszystkich punktów zwrotnych rynku, do określenia momentu zawarcia transakcji kupna lub sprzedaży w punktach, w których nie występuje sygnał Carolana, niezbędna jest dodatkowa metoda, którą w dalszej części pracy będziemy nazywać pomocniczą. Doskonale do tego celu nadaje się jedna z podstawowych zasad współczesnej analizy technicznej trendu, zgodnie z którą "trend jest kontynuowany, dopóki nie pojawią się definitywne oznaki świadczące o jego odwróceniu20". Inaczej mówiąc, istniejący trend wykazuje tendencję do kontynuacji swojego dotychczasowego kierunku. Oczywiście sygnał zmiany trendu może nastąpić w każdej chwili, ale dopóki nie następuje, gracz giełdowy musi szanować ustalony trend. O zmianie trendu ze wzrostowego na spadkowy będziemy mówić wtedy, gdy kolejna zwyżka (punkt C - rys. 11) nie zdoła przekroczyć poprzedniego szczytu (punkt A), a kolejna zniżka cen (punkt D) przełamała poziom dołka występującego po pierwszym szczycie (punkt B). W tym przypadku sygnał sprzedaży zostaje wygenerowany w momencie przebicia poziomu pierwszego dołka (punkt S). Zmiana trendu spadkowego na wzrostowy występuje, gdy kolejna zniżka (punkt C) nie zdoła przekroczyć poprzedniego dołka (punkt A), a kolejna zwyżka cen (punkt D) przebije szczyt występujący po pierwszym dołku (punkt B) Sygnał kupna zostanie utworzony w momencie przebicia pierwszego szczytu (punkt K21).
Rysunek 11. Ilustracja trendu spadkowego i wzrostowego wg teorii Dowa. Sygnał sprzedaży otrzymujemy w punkcie S, a kupna w K
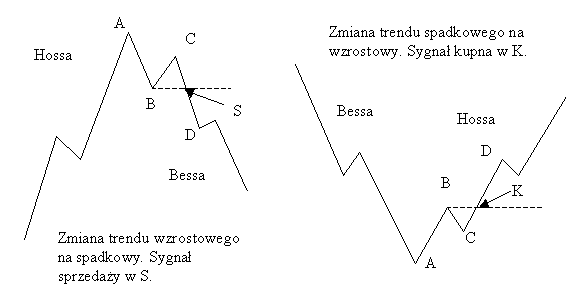
źródło: opracowanie własne
Istotne znaczenie przy podejmowaniu decyzji o otwarciu lub likwidacji posiadanych pozycji będą miały dla nas także sygnały Ci nie tworzące okienek Carolana i sygnały Fischera.
Transakcje z wykorzystaniem okienek Carolana zostały przeprowadzone wg następujących założeń:
- Wszelkie obliczenia dotyczące inwestycji na GPW dokonane zostały wyłącznie w oparciu o ceny zamknięcia
- Brak kosztów transakcji
- Brak konieczności gwarantowania transakcji poprzez wnoszenie wkładu zabezpieczającego (margin requirements) - założenie to dotyczy pozycji krótkich
- Doskonała podzielność akcji
- Poprzez inwestycje na rynku akcji rozumie się taki dobór składników portfela, który odpowiada kompozycji indeksu WIG w momencie przeprowadzania transakcji. Aktualnie dopuszczone zostały do obrotu giełdowego instrumenty finansowe posiadających wiele cech akcji, lecz nie będące akcjami sensu stricto, natomiast umożliwiających otwieranie pozycji na indeksie WIG20 przy pomocy jednego zlecenia, a nie kompozycji zleceń na akcje poszczególnych spółek wchodzących w skład indeksu określonej liczby. Instrument ten nosi nazwę MiniWIG2022
- Pozycja zostaje zlikwidowana w sytuacji odmiennego od oczekiwanego rozwoju sytuacji na rynku i wystąpienia zmiany trendu opisanego powyżej jako metody pomocniczej lub w szczególnych przypadkach zmiany trendu w pobliżu punktów zwrotnych Ci lub sygnałów Fischera
- Przy obliczaniu zakumulowanej stopy zwrotu z poszczególnych transakcji zakłada się, że środki finansowe dostępne po zamknięciu transakcji pierwszej są w całości angażowane w transakcji następnej
Uzyskane wyniku przedstawione zostały w tabeli nr 6 i na rys. nr 12.
Tabela 6.1 Wyniki systemu inwestycyjnego opartego na okienkach Carolana i sygnałach Fischer
K
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
27.12.2001
13764,52
0,00%
Okienko Carolana
S
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
04.01.2002
15013,22
9,07%
Okienko Carolana
K
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
16.01.2002
15652,81
4,26%
Okienko Carolana
S
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
25.01.2002
16311,6
4,21%
Sygnał Fischera
K
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
12.02.2002
15289,83
-6,26%
Okienko Carolana
S
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
18.02.2002
15259,44
-0,20%
Po przebiciu dołka
K
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
21.02.2002
15071,76
-1,23%
Okienko Carolana
S
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
04.03.2002
15466,66
2,62%
Okienko Carolana
K
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
14.03.2002
15244,1
-1,44%
Okienko Carolana
S
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
25.03.2002
14935,32
-2,03%
Okienko Carolana
K
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
10.05.2002
14931,81
-0,02%
Okienko Carolana
S
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
07.06.2002
15558,81
4,20%
Sprzedaż po wystąpieniu sygnału c12
K
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
19.07.2002
13320,2
-14,39%
Okienko Carolana
S
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
23.07.2002
13117,83
-1,52%
Po przebiciu dołka
K
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
21.08.2002
13326,65
1,59%
Sygnał Fischera
S
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
03.09.2002
12966,93
-2,70%
Sygnał Fischera
K
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
10.10.2002
12893,1
-0,57%
Okienko Carolana
S
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
09.12.2002
14726,38
14,22%
Okienko Carolana
K
Data
Wig
Zmiana Wig
Uwagi dotyczące przeprowadzenia transakcji
27.12.2002
14402,55
-2,20%
Sygnał Fischera
|
K - kupno, S - sprzedaż |
Data | Wig | Zmiana Wig | Uwagi dotyczące przeprowadzenia transakcji |
|---|---|---|---|---|
| K | 27.12.2001 | 13764,52 | 0,00% | Okienko Carolana |
| S | 04.01.2002 | 15013,22 | 9,07% | Okienko Carolana |
| K | 16.01.2002 | 15652,81 | 4,26% | Okienko Carolana |
| S | 25.01.2002 | 16311,6 | 4,21% | Sygnał Fischera |
| K | 12.02.2002 | 15289,83 | -6,26% | Okienko Carolana |
| S | 18.02.2002 | 15259,44 | -0,20% | Po przebiciu dołka |
| K | 21.02.2002 | 15071,76 | -1,23% | Okienko Carolana |
| S | 04.03.2002 | 15466,66 | 2,62% | Okienko Carolana |
| K | 14.03.2002 | 15244,1 | -1,44% | Okienko Carolana |
| S | 25.03.2002 | 14935,32 | -2,03% | Okienko Carolana |
| K | 10.05.2002 | 14931,81 | -0,02% | Okienko Carolana |
| S | 07.06.2002 | 15558,81 | 4,20% | Sprzedaż po wystąpieniu sygnału c12 |
| K | 19.07.2002 | 13320,2 | -14,39% | Okienko Carolana |
| S | 23.07.2002 | 13117,83 | -1,52% | Po przebiciu dołka |
| K | 21.08.2002 | 13326,65 | 1,59% | Sygnał Fischera |
| S | 03.09.2002 | 12966,93 | -2,70% | Sygnał Fischera |
| K | 10.10.2002 | 12893,1 | -0,57% | Okienko Carolana |
| S | 09.12.2002 | 14726,38 | 14,22% | Okienko Carolana |
| K | 27.12.2002 | 14402,55 | -2,20% | Sygnał Fischera |
Tabela 6.2 Wyniki systemu inwestycyjnego opartego na okienkach Carolana i sygnałach Fischer
K
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-
-
-
0,00%
-
S
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
9,07%
9,07%
-
0,00%
9,07%
K
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-
9,07%
-4,26%
-4,26%
4,43%
S
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
4,21%
13,66%
-
-4,26%
8,82%
K
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-
13,66%
6,26%
1,74%
15,64%
S
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-0,20%
13,43%
-
1,74%
15,40%
K
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-
13,43%
1,23%
2,99%
16,82%
S
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
2,62%
16,41%
-
2,99%
19,88%
K
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-
16,41%
1,44%
4,47%
21,61%
S
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-2,03%
14,05%
-
4,47%
19,15%
K
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-
14,05%
0,02%
4,49%
19,17%
S
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
4,20%
18,84%
-
4,49%
24,18%
K
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-
18,84%
14,39%
19,53%
42,04%
S
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-1,52%
17,03%
1,52%
19,53%
39,89%
K
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-
17,03%
-1,59%
17,62%
37,66%
S
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-2,70%
13,87%
-
17,63%
33,94%
K
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
-
13,87%
0,57%
18,29%
34,71%
S
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
14,22%
30,07%
-
18,30%
53,86%
K
Stopa zwrotu z pojedynczej transakcji pozycja długa
Zakumulowana stopa zwrotu - pozycja długa
Stopa zwrotu z pojedynczej transakcji pozycja krótka
Zakumulowana stopa zwrotu - pozycja krótka
Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka
30,07%
2,20%
20,90%
57,24%
|
K - kupno, S - sprzedaż |
Stopa zwrotu z pojedynczej transakcji pozycja długa | Zakumulowana stopa zwrotu - pozycja długa | Stopa zwrotu z pojedynczej transakcji pozycja krótka | Zakumulowana stopa zwrotu - pozycja krótka | Zakumulowana stopa zwrotu - pozycja długa + pozycja krótka |
|---|---|---|---|---|---|
| K | - | - | - | 0,00% | - |
| S | 9,07% | 9,07% | - | 0,00% | 9,07% |
| K | - | 9,07% | -4,26% | -4,26% | 4,43% |
| S | 4,21% | 13,66% | - | -4,26% | 8,82% |
| K | - | 13,66% | 6,26% | 1,74% | 15,64% |
| S | -0,20% | 13,43% | - | 1,74% | 15,40% |
| K | - | 13,43% | 1,23% | 2,99% | 16,82% |
| S | 2,62% | 16,41% | - | 2,99% | 19,88% |
| K | - | 16,41% | 1,44% | 4,47% | 21,61% |
| S | -2,03% | 14,05% | - | 4,47% | 19,15% |
| K | - | 14,05% | 0,02% | 4,49% | 19,17% |
| S | 4,20% | 18,84% | - | 4,49% | 24,18% |
| K | - | 18,84% | 14,39% | 19,53% | 42,04% |
| S | -1,52% | 17,03% | 1,52% | 19,53% | 39,89% |
| K | - | 17,03% | -1,59% | 17,62% | 37,66% |
| S | -2,70% | 13,87% | - | 17,63% | 33,94% |
| K | - | 13,87% | 0,57% | 18,29% | 34,71% |
| S | 14,22% | 30,07% | - | 18,30% | 53,86% |
| K | 30,07% | 2,20% | 20,90% | 57,24% |
źródło: opracowanie własne
Łączna zakumulowana stopa zwrotu dla transakcji przeprowadzonych na przestrzeni 2002 r.:
- z wykorzystaniem pozycji długich przyniosła stopę zwrotu w wysokości 30,07%
- z wykorzystaniem pozycji krótkich przyniosła stopę zwrotu w wysokości 20,90%
- z wykorzystaniem zarówno pozycji długich jak i krótkich stopę zwrotu w wysokości 57,24%
Na przestrzeni analizowanego okresu:
- łączna zmiana indeksu WIG wyniosła 3,19%
- stopa zwrotu uzyskana w tym samym czasie przez najlepszy fundusz akcyjny tj. Skarbiec Akcja ukształtowała się na poziomie 8,21%
- benchmark23 dla funduszy akcyjnych składający się w 90% z indeksu Wig a w 10% ze średniej rentowności 13 tygodniowym bonów skarbowych z przetargów wyniósł 3,72%
- stopa zwrotu uzyskana w tym samym czasie przez najlepszy fundusz zrównoważony tj. Skarbiec Waga ukształtowała się na poziomie 11,88%
- benchmark24 dla funduszy zrównoważonych składający się w 50% z indeksu Wig a w 50% ze średniej rentowności 52 tygodniowym bonów skarbowych z przetargów wyniósł 5,73%
- stopa zwrotu uzyskana w tym samym czasie przez najlepszy fundusz stabilnego wzrostu tj. Skarbiec II Filar ukształtowała się na poziomie 17,13%
- benchmark25 dla funduszy stabilnego wzrostu składający się w 30% z indeksu Wig a w 70% ze średniej rentowności 52 tygodniowym bonów skarbowych z przetargów wyniósł 6,74%
- stopa zwrotu uzyskana w tym samym czasie przez najlepszy fundusz obligacji tj. ING Obligacji 2 ukształtowała się na poziomie 21,25%
- benchmark26 dla funduszy obligacji składający się w 100% ze średniej rentowności 52 tygodniowym bonów skarbowych z przetargów wyniósł 8,26%
- stopa zwrotu uzyskana w tym samym czasie przez najlepszy fundusz pieniężny tj. Unikorona Rynku Pieniężnego ukształtowała się na poziomie 10,49%
- benchmark27 dla funduszy zrównoważonych składający się 100% ze średniej rentowności 13 tygodniowym bonów skarbowych z przetargów wyniósł 8,49%
Łącznie przeprowadzonych zostało 9 transakcji z wykorzystaniem pozycji długiej i krótkiej. Całkowity czas utrzymywania akcji w pozycji długiej wyniósł 148 dni, a w pozycji krótkiej 212 dni tj. prawie dwukrotnie dłużej. Dla pozycji długich aż 4 transakcje zakończyły się ujemną stopą zwrotu. W przypadku pozycji krótkich ujemną stopę zwrotu odnotowano jedynie dla dwu transakcji. Maksymalna stopa zwrotu z pojedynczej transakcji ukształtowała się na poziomie nieco większym niż 14% zarówno dla pozycji długich jak i krótkich. Natomiast maksymalna strata z pojedynczej transakcji nie przekroczyła 5%. Przyjmując średnią rentowność lokat na rynku bezpiecznych instrumentów finansowych na poziomie benchmarku dla funduszy obligacji możemy obliczyć stopę zwrotu, jaką inwestor dodatkowo osiągnąć inwestując posiadane środki na rynku pieniężnym w okresach, kiedy nie utrzymywał otwartej pozycji:
- w przypadku pozycji długich liczba dni utrzymywania gotówki była równa: 365-148=217 dni. Osiągnięta w tym okresie dodatkowa stopa zwrotu wyniosłaby
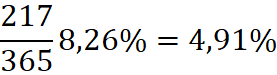 co daje łączną zakumulowaną stopę z pozycji długich równą 36,46%.
co daje łączną zakumulowaną stopę z pozycji długich równą 36,46%. - w przypadku pozycji krótkich liczba dni utrzymywania gotówki była równa 365-212=153 dni. Osiągnięta w tym okresie dodatkowa stopa zwrotu wyniosłaby
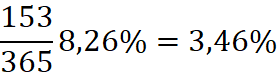 co daje łączną zakumulowaną stopę z pozycji długich równą 25,09%.
co daje łączną zakumulowaną stopę z pozycji długich równą 25,09%.
Rysunek 12. Zakumulowana stopa zwrotu dla transakcji dokonanych z wykorzystaniem wskazań okienek Carolana i sygnałów Fischera
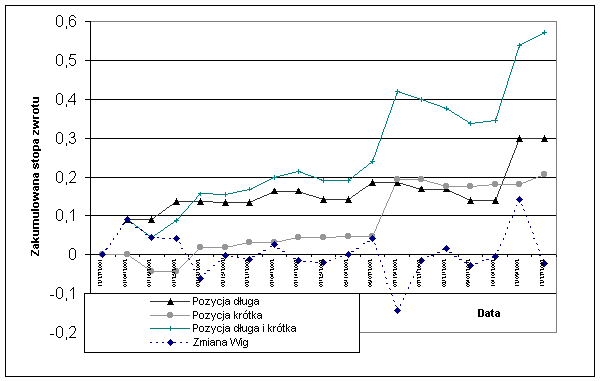
źródło: opracowanie własne
Podsumowanie
Strategia inwestycyjna oparta o wskazania okienek Carolana i metody Fischera przyniosła znacznie wyższą stopę zwrotu niż inwestycje w bezpieczne instrumenty finansowe. Godnym podkreślenia jest fakt, że rok 2002 r. cechował się dużą rentownością instrumentów dłużnych. Strategia inwestycyjna oparta o wskazania okienek Carolana i Fischera może być przeniesiona na rynek kontraktów terminowych na indeks Wig20, silnie skorelowany z indeksem Wig.
Referencje
- Oster L. "Astronomia współczesna", PWN, Warszawa 1986.
- Ciąg Fibonacciego i znaczenie liczby F na rynkach finansowych zostało przedstawione w pracy: Borowski K., Nowakowski J. "Wykorzystanie ciągów liczbowych w analizie technicznej", Studia i prace Kolegium Zarządzania i Finansów - Zeszyt 20, Warszawa 2001.
- Carolan C. "Kalendarz spiralny", WIG-Press, Warszawa 1996. Koncepcję okienek czasowych jako przedziału czasu oznaczającego cykliczny szczyt lub dołek cen - spotykamy także w: Plummer T. "Psychologia rynków finansowych", WIG - Press, Warszawa 1995.
- Carolan C. "Kalendarz spiralny", WIG-Press, Warszawa 1996.
- Problem ten zostanie poruszony w dalszej części pracy
- Jeśli X jest dowolnym, niepustym zbiorem. Funkcję
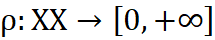
nazywamy metryką w zbiorze X, gdy spełnia następujące warunki:
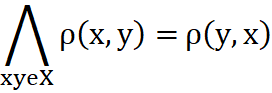
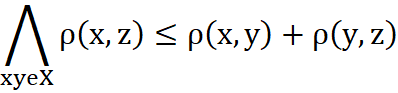
Na podstawie Krzyszkowski J., Turdza E. "Elementy topologii", Wydawnictwo Naukowe, Kraków 1996. - Elder A. "Zawód inwestor giełdowy", Dom Wydawniczy ABC, Warszawa 1998.
- Frost A., Pretcher R. "Teoria fal Elliotta", WIG-Press, Warszawa 1995.
- Fischer R. "The Golden Section Compass Seminar", Fibonacci Trading, P.O. Box HM 1653, Hamilton 5, Bermuda USA, Bermuda 1983.
- Fischer R. "Liczby Fibonacciego na giełdzie", WIG - Press, Warszawa 1996.
- Fischer R. "Liczby Fibonacciego na giełdzie", WIG - Press, Warszawa 1996.
- Fischer R. "Liczby Fibonacciego na giełdzie", WIG - Press, Warszawa 1996.
- Fischer R. "Liczby Fibonacciego na giełdzie", WIG - Press, Warszawa 1996.
- Gately E. "Cena i czas", WIG - Press, Warszawa 1999.
- Nature Pulse stworzony przez amerykańską firmę Kasanjian Research, P. O. Box 4608, Blue Jay, CA 92317-4608. Strona internetowa: http://www.kasanjianresearch.com/ z dnia 04.10.2002.
- Fibonacci Trader jest programem napisanym przez amerykańską firmę o tej samej nazwie. Strona internetowa: http://www.fibonaccitrader.com z dnia 04.10.2002.
- Teoria R. Fischera jest datowana na 1983 r., natomiast C. Carolana - na 1996 r.
- Tarczyński W. "Rynki kapitałowe", Agencja Wydawnicza Placet, Warszawa 2001.
- Carolan C. "Kalendarz spiralny", WIG-Press, Warszawa 1996.
- Murphy J. "Analiza techniczna", WIG - Press, Warszawa 1995.
- Zagadnienie to zostało doskonale opisane w pracach:
Komar Z. "Sztuka spekulacji", Wydawnictwo PRET, Warszawa 1993.
Tharp K. "Poradnik spekulanta", WIG - Press, Warszawa 2000.
Kaufman P. "Smarter Trading: Improving Performance in Changing Markets", Mc Graw - Hill, New York 1995. - Na podstawie strony internetowej: http://www.gpw.com.pl/xml/papiery/pochodne/miniwig20.xml?sekcja=3 z dnia 31.12.2001.
- Świderek T. "Obligacje znów najlepsze", Rzeczpospolita z dnia 3.01.2003 str. B5.
- Świderek T. "Obligacje znów najlepsze", Rzeczpospolita z dnia 3.01.2003 str. B5.
- Świderek T. "Obligacje znów najlepsze", Rzeczpospolita z dnia 3.01.2003 str. B5.
- Świderek T. "Obligacje znów najlepsze", Rzeczpospolita z dnia 3.01.2003 str. B5.
- Świderek T. "Obligacje znów najlepsze", Rzeczpospolita z dnia 3.01.2003 str. B5.
Krzysztof Borowski, Jerzy Nowakowsk
Niniejszy materiał, przygotowany przez DM BOŚ S.A. ma charakter wyłącznie informacyjny, prezentowany jest w celach edukacyjnych i nie stanowi porady prawnej oraz nie jest rekomendacją osobistą w ramach świadczenia usługi doradztwa inwestycyjnego zgodnie z przepisami prawa. DM BOŚ S.A. nie udziela gwarancji dokładności, aktualności, oraz kompletności niniejszych informacji. Zaleca się przeprowadzenie we własnym zakresie niezależnego przeglądu informacji z niniejszego materiału.


