Ponieważ pomiędzy czynnikami wpływającymi na cenę opcji zachodzą kolejne interakcje, dla celów analitycznych wprowadzono zmienne które je opisują. W żargonie zawodowym nazywane są "greeks" ponieważ oznaczone są literami greckiego alfabetu. Ich znaczenie jest następujące:
Delta - mierzy wielkość zmiany ceny opcji w zależności od ceny instrumentu bazowego (underlying). Zatem dla opcji call Delta jest dodatnia natomiast dla opcji put Delta jest ujemna.
Warto zwrócić uwagę, że Delta zmienia się w czasie życia opcji. Ogólna zasada mówi, że im bliżej terminu wygaśnięcia opcji, tym Delta będzie zbiegać do 1 dla opcji call ITM (in-the-money) oraz do -1 dla opcji put ITM. W przypadku opcji OTM im bliżej terminu wygaśnięcia tym Delta będzie bliższa 0 - zmiana ceny instrumentu bazowego będzie coraz słabiej wpływać na cenę opcji OTM.
Przykład 1
Opcja put OTM na WIG20 - OW20O6210 była notowana 19.12.2005 po cenie 4,4 pkt. Następnego dnia jej cena wyniosła - 3,5 pkt. Czyli zmiana wyniosła -0,9 pkt
Tymczasem indeks WIG20 zmienił swoją wartość o 37,73 pkt, z 2604,88 (19.12.2005) na 2642,61 (20.12.2005). Delta dla opcji OW20O6210 wynosi więc -0,02 co można interpretować, iż zmiana WIG20 o 100 pkt. przyniesie zmianę ceny opcji o 2 pkt.
Poniższa tabelka przedstawia zmianę premii oraz zmianę ceny instrumentu bazowego dla opcji call ITM na akcje KGHM OKGHC6055.
19.12.2005
20.12.2005
Zmiana
Delta
Akcje KGHM
59,7
61
1,3
-
Opcja OKGHC6055
6,5
7,4
0,9
0,9/1,3 = 0,69
| 19.12.2005 | 20.12.2005 | Zmiana | Delta | |
| Akcje KGHM | 59,7 | 61 | 1,3 | - |
| Opcja OKGHC6055 | 6,5 | 7,4 | 0,9 | 0,9/1,3 = 0,69 |
źródło: obliczenia własne
Delta wyniosła więc 0,69 czyli zmiana ceny akcji o 1 PLN spowodowała zmianę w wartości premii o 0,69 zł
UWAGA! - wszystkie przytoczone poniżej przykłady z użyciem wykresów Programu Option Investigator przedstawione są dla opcji na akcje, gdzie minimalny kontrakt opcyjny odnosi się do pakietu akcji 100 sztuk, dlatego też przedstawione wartości współczynników są odpowiednio przemnożone przez 100.
Przykład 2
Delta równoważących się pozycji jest równa 0. Dla akcji Y notowanej po 50 kupujemy jedną opcję call 50 i jedną opcję put 50 (wykres 1).
Wykres 1 Wykres zysków i strat dla pozycji neutralnej
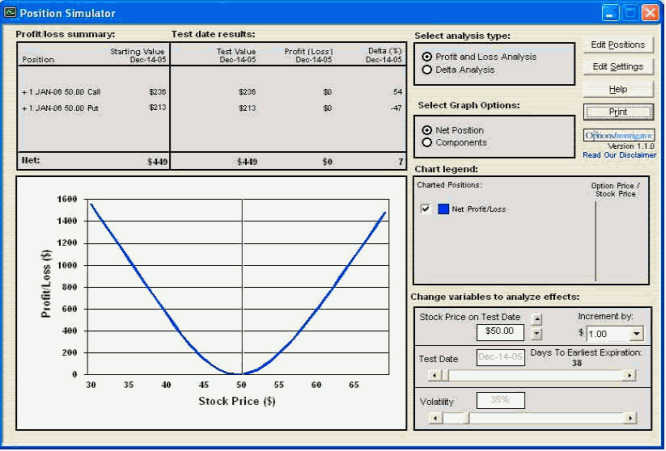
źródło: obliczenia własne przy pomocy programu Option Investigator
Teoretycznie Delta takiego układu jest równa zero (w naszym przykładzie realna Delta=7 wynika z zaokrągleń stosowanych przez program), zatem pozycja jest neutralna - jej zyskowność nie jest oparta na jednym kierunku rynku. Jeżeli jednak dokupimy dodatkowo opcję put 50 to suma Delta tej pozycji wyniesie -40 (wykres 2) co oznacza że jeżeli cena akcji Y będzie spadać, to nasza pozycja przyniesie nam większy zysk w krótszym czasie niż w przypadku wzrostu kursu Y.
Wykres 2 Wykres zysków i strat dla Delty ujemnej
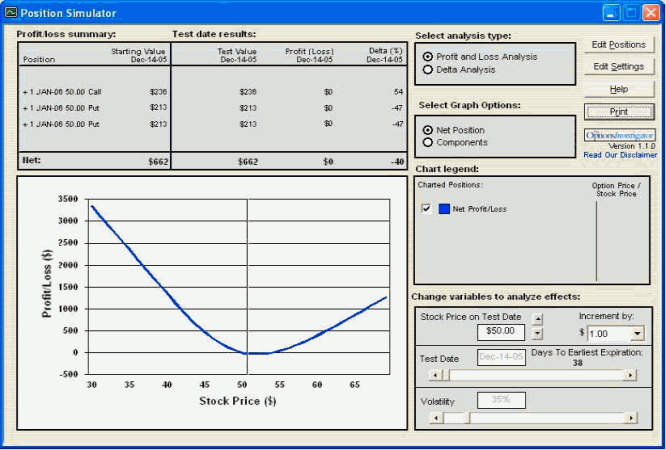
źródło: obliczenia własne przy pomocy programu Option Investigator
Gamma - mierzy wielkość zmiany Delta modelu teoretycznego opcji w zależności od ceny instrumentu bazowego. W tym punkcie zwracam uwagę, że Delta jak i Gamma nie są wartościami stałymi i jakakolwiek zmiana jednego z sześciu czynników wpływających na cenę opcji spowoduje zmianę zarówno Delta jak i Gamma.
Przykład 3
Opcja call dla indeksu X o kursie 2600 ma Delta=0,6 oraz Gamma =0,05. Wobec tego zmiana wartości indeksu o jeden punkt spowoduje zmianę wartości Delta o 0,05. Dlatego jeżeli indeks wzrośnie o 1 punkt, Delta powinna wynieść 0,65, jeżeli zaś wartość indeksu zmniejszy się o jeden punkt, teoretyczna wartość Delta wyniesie 0,55.
Przykład 4
Wykresy 3 i 4 przedstawiają zmianę wartości premii opcji w zależności od Gamma. Załóżmy, że 14 grudnia 2005 (wykres 3) przy cenie instrumentu bazowego $50 kupujemy trzy opcje call: ITM o cenie wykonania (strike price) $40, ATM o cenie wykonania (strike price) $50 oraz opcję OTM o cenie wykonania (strike price) $70.
Wykres 3 Rozkład zysków i strat dla opcji call
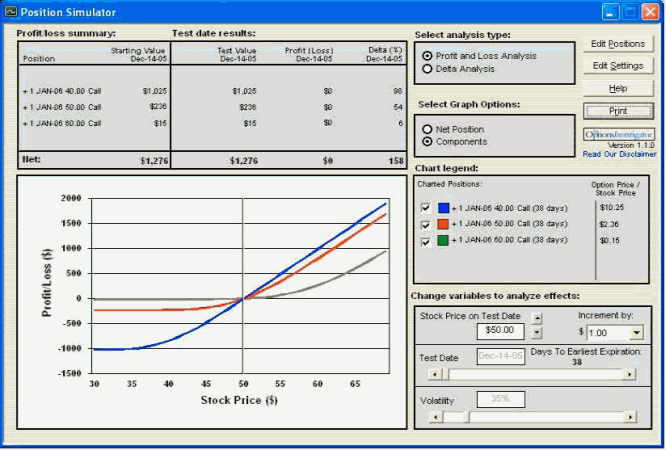
źródło: obliczenia własne przy pomocy programu Option Investigator
Za pomocą modułu Option Simulator tworzymy scenariusz w którym cena akcji Y wzrasta o $10 w ciągu 8 dni (wykres 4). Z zestawienia wynika wyraźnie, że najwyższy przyrost procentowy premii nastąpił dla opcji call 60. Przede wszystkim dlatego, że na wykresie 3 najwyższą wartość Gamma miała opcja call 50 ale wskutek wzrostu kursu na wykresie 4 najwyższe Gamma ma opcja call 60.
Wykres 4 Rozkład zysków i strat dla opcji call po zmianie ceny instrumentu bazowego o $10 po 8 dniach
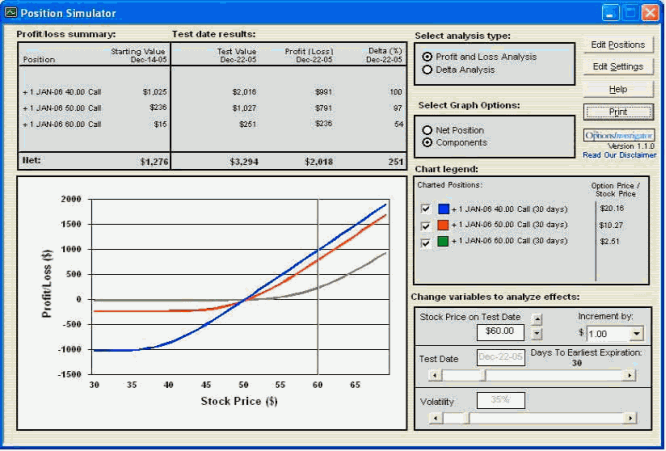
źródło: obliczenia własne przy pomocy programu Option Investigator
Dla inwestora najważniejszą kwestią jest fakt, że Gamma jest najwyższa dla opcji ATM (at-the-money). Zarówno dla opcji OTM jak i ITM Gamma jest niższa. Oznacza to, że jeżeli kurs zmienia się i opcja przechodzi z poziomu OTM w ITM lub odwrotnie, tempo zmiany Delta będzie wzrastać do punktu ATM, a następnie będzi e spadać bez względu na to, jaki typ opcji badamy (call czy put), jak również niezależnie od kierunku zmiany ceny instrumentu bazowego.
Druga ważną kwestię, którą należy tu odnotować to to, że zarówno dla opcji call jak i put o tej samej cenie wykonania (strike price) oraz o tej samej dacie wygasania (expiration date) Gamma ma taką samą wartość .
Vega - mierzy zmianę ceny opcji w powiązaniu ze zmiennością instrumentu bazowego, a dokładniej określa zmianę ceny opcji wobec wzrostu zmienności o jeden procent.
Przykład 5
Opcja o Vega 0,20 straci 0,2 pkt. w przypadku spadku zmienności instrumentu bazowego o 1%, oraz zyska 0,2 centów wobec wzrostu zmienności o 1%.
Przykład 6
Biorąc pod uwagę portfel opcji wskazany w przykładzie 4 powiększony o kupno opcji call 50 o dacie wygasania (expiration date) w kwietniu 2006 roku (wykres 5) śledzimy zachowanie opcji w przypadku wzrostu zmienności.
Wykres 5 Rozkład zysków i strat dla opcji call o różnych terminach wygasania

źródło: obliczenia własne przy pomocy programu Option Investigator
Nasz scenariusz (wykres 6) zakłada wzrost zmienności o 10 p.p. (z 35% do 45%) w ciągu kolejnych 8 dni przy jednoczesnym utrzymaniu kursu instrumentu bazowego na tym samym poziomie $50.
Wykres 6 Rozkład zysków strat dla opcji call o różnych terminach wygasania przy zmianie zmienności instrumentu bazowego o 10 p.p.
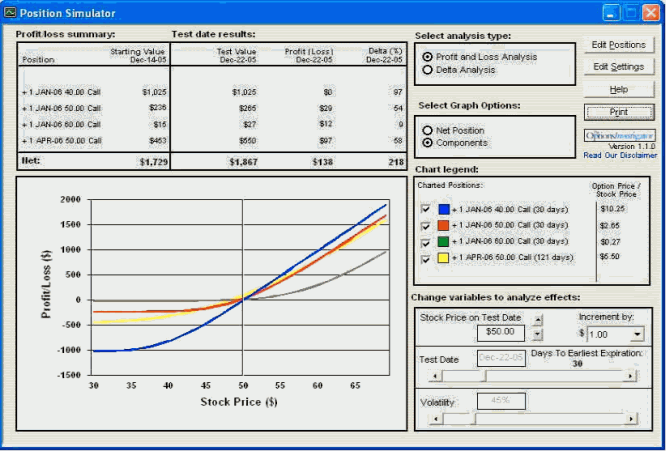
źródło: obliczenia własne przy pomocy programu Option Investigator
Widać wyraźnie, że najbardziej wzrosła cena opcji OTM oraz opcji ATM o dalszym terminie wygasania (expiration date). Jest to całkowicie logiczne - w przypadku ruchu cen te właśnie opcje mają szanse na największy zysk. W przypadku większej zmiany cen OTM call 60 ma szansę wejść na poziom ATM i mieć najwyższe Gamma oraz ATM call 50 wygasająca w kwietniu, jako że ta opcja ma więcej czasu niż inne żeby przynieść zysk.
W odróżnieniu od opisanych wyżej współczynników, Vega zależy od czynnika (zmienność), który nie daje się obserwować, a powstaje w wyniku kalkulacji. Dlatego też Vega zachowuje się inaczej niż Delta i Gamma - jej wartość nigdy nie jest stała. Vega zmienia się ciągle wraz ze zmianą pozostałych współczynników przybierających nowe wartości zależnie od zmiany czynników cenotwórczych.
Dla językoznawców wyjaśnienie - vega nie jest literą greckiego alfabetu, ale nazwa ta została przyjęta ze względu na powiązanie z wielkością do jakiej się odnosi: Vega - Volatility (zmienność).
Dla inwestora najważniejsze wnioski to:
- cena opcji może zmienić- się znacznie w przypadku wzrostu lub spadku zmienności,
- zmiana ceny opcji w odniesieniu do Vega jest inna dla opcji OTM, ATM oraz ITM,
- zmiana ceny jest o wiele większa dla opcji o dalszej dacie wygasania (expiration date) niż dla opcji o mniejszej wartości czasu (time premium), czyli o bliższej dacie wygaśnięcia.
Ponieważ zmienność ma duże znaczenie dla inwestowania w opcje oraz kalkulacji ich wartości teoretycznej, zajmiemy się tym tematem szerzej w jednym z kolejnych odcinków KO.
Theta - określa zmianę wartości modelu teoretycznego opcji wobec upływu czasu. Jedną z najważniejszych cech opcji jest jej "ograniczona żywotność". Każda opcja ma datę wygaśnięcia (expiration date), po której opcja musi zostać wykonana (w przypadku ITM) albo wygasa bez wartości. Theta określa spadek wartości opcji przypadający na jednostkę czasu. Wobec tego Theta ma podobne zależności jak Delta i Gamma - zmiana jednego z czynników cenotwórczych powoduje zmianę Theta.
Przykład 7
Ponownie użyjemy tej samej pozycji wyjściowej, którą wykorzystaliśmy w przykładzie 6. Tym razem jednak prześledzimy zachowanie opcji pod kątem upływu czasu bez zmiany kursu instrumentu bazowego (wykres 7).
Wykres 7 Rozkład zysków i strat dla opcji call o różnych terminach wygasania
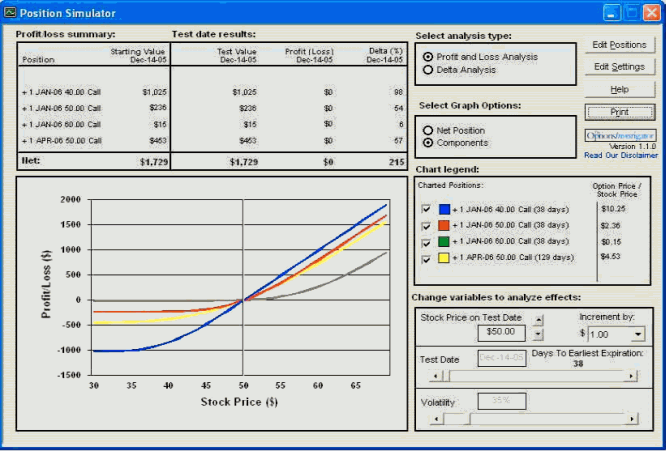
źródło: obliczenia własne przy pomocy programu Option Investigator
Symulator ustawiamy w przyszłość, na dzień 16 stycznia 2006 (wykres 8), 5 dni przed wygasaniem opcji styczniowych. Tutaj najmniejszą "szkodę" poniosła opcja ITM call 40, jako że jej wartość wewnętrzna (intrinsic value) jest najwyższa, a wartość czasu (time premium) najniższa. Trzymając się tego klucza łatwo wytłumaczyć spadek premii pozostałych opcji - OTM call 60 ma niewielkie szanse na zysk, natomiast szansa na zysk opcji ATM January 06 call 50 jest mniejsza niż ITM, ale wciąż realna.
Dla porównania opcja ATM o dalszej dacie wygasania, April 06 call 50 straciła stosunkowo niewiele - jej cena wykonania (strike price) jest blisko kursu, a wciąż ma wiele czasu przed sobą na realizację zysku.
Wykres 8 Rozkład zysków i strat dla opcji call o różnych terminach wygasania po upływie 33 dni
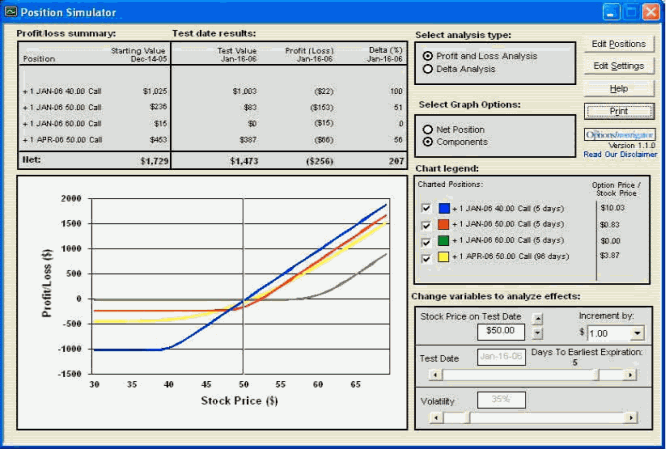
źródło: obliczenia własne przy pomocy programu Option Investigator
Inwestor powinien zwrócić tutaj uwagę na fakt, że Theta zmienia się stale - w miarę upływu czasu, wartość czasu opcji (time value) ulega coraz szybszej erozji, aż do momentu wygaśnięcia. Jedynie opcje ITM posiadają wartość wynikająca z egzekucji prawa opcji na podstawie różnicy pomiędzy kursem zamknięcia instrumentu bazowego (underlying) a ceną wykonania (strike price). Opcje ATM oraz OTM nie posiadają żadnej wartości wskutek utraty wartości czasu (time premium).
Dlatego opcje ATM/OTM bez względu na to jakie ceny przyjmują wcześniej, w momencie wygaśnięcia zawsze mają tę samą wartość, a mianowicie 0.
Podstawowe techniki
Nie ma takiego źródła na świecie, które by zawierało wszystkie techniki zastosowania opcji. Co więcej - wciąż powstają nowe, mniej lub bardziej złożone i wiele z nich przynosi efekty nieporównywalne z jakimikolwiek instrumentami finansowymi.
Opcje mogą przynosić zyski w KAŻDYCH warunkach rynkowych: silnych lub słabych trendach zwyżkowych lub zniżkowych, w czasie trendu horyzontalnego oraz w czasach najprzeróżniejszych kombinacji wyżej wymienionych.
Literatura przedmiotu opisuje zazwyczaj kilkadziesiąt technik podstawowych, ale kiedy dodamy do tego możliwości łączenia ich między sobą, łączenia z instrumentem bazowym lub kontraktami terminowymi na ten instrument, możliwości kombinacji wzrastają logarytmicznie. Do tego dochodzą konwersje pozycji kompleksowych w inne - wszystko to razem tworzy ocean możliwości, w którym odpowiednie zastosowanie wybranych technik do warunków rynku może przynosić sukces nieporównywalny z technikami opartymi na innych instrumentach finansowych.
Przegląd rozpoczynamy od prostych technik kierunkowych (zyskownych dla rynku o zdecydowanym trendzie).
Long call/put
Najprostsza z możliwych technika kierunkowa użycia opcji. Kupujemy opcję call w oczekiwaniu na zwyżkę, lub opcję put w oczekiwaniu na zniżkę. Główna zaleta strategii w porównaniu z użyciem akcji lub kontraktu terminowego polega na tym, że nasza decyzja nie musi mieć w tym momencie 100% trafności co do kierunku. Cena może zniżkować, może przejść w trend horyzontalny, jeśli jednak w czasie "życia" opcji będzie wzrastać (lub maleć w przypadku opcji put) w przewidzianym przez nas kierunku, wtedy mamy szansę na osiągnięcie zysku. Niestety, nie jest to duża szansa, jako że opcja ma swoją wartość i wzrost lub spadek kursu musi wpierw zrównoważyć cenę jaką zapłaciliśmy za opcję, zanim cokolwiek zaczniemy zarabiać.
Wykres 9 Rozkład zysków i strat dla opcji call 100 z premią 492
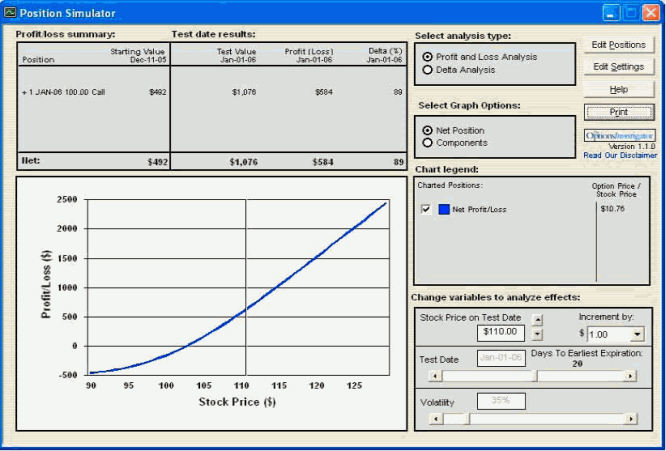
źródło: obliczenia własne przy pomocy programu Option Investigator
Long stock (future)/long put
Short stock (future)/long call
Technika zakłada kupno instrumentu bazowego (ew. kontraktów futures na ten instrument) i jednoczesnym kupnie opcji put na ten instrument lub sprzedaży instrumentu (sprzedaży kontraktów na ten instrument) przy jednoczesnym kupnie opcji na niego.
Można ją uznać za zdecydowanie lepszą technikę kierunkową od poprzedniej. W tym momencie nasza pozycja w instrumencie bazowym jest całkowicie zabezpieczona w czasie "życia" opcji..
Pomimo że ponownie mamy do czynienia z malejącą wartością czasu (time value) opcji zabezpieczającej pozycję, technika ta ma sens np. w czasie wchodzenia na początek trendu jako alternatywa do tradycyjnego wejścia z użyciem zlecenia stop oraz stopu ruchomego.
Pomimo że od strony technicznej strategia jest niemalże identyczna jak poprzednia, chciałbym tutaj zwrócić uwagę, że na strategie opcyjne należy patrzeć nie tylko przez pryzmat analiz zachowania rynku ale także pod kątem elastyczności i możliwości przekształceń istniejącej pozycji w inną. W opisanym przypadku gdy cena znajdzie się w pewnej odległości od ceny wykonania (strike price) opcji zabezpieczającej możemy ją sprzedać, zastępując ją zwykłym zleceniem stop i następnie przesuwać je, tak jak robimy to w przypadku używania stopu ruchomego, czyli zlecenia stop poruszającego się za rynkiem.
Przykład 8
11 grudnia 2005 instrument Y osiągnął cenę $100. Ponieważ wiadomości napływające na giełdę są optymistyczne, Inwestor A kupuje opcję call o cenie wykonania $100 w oczekiwaniu na dalszą zwyżkę ceny, natomiast Inwestor B, który ma te same oczekiwania kupuje 100 akcji Y oraz zabezpiecza pozycję przez kupno opcji put o cenie wykonania (strike price) 100.
Oczekiwania inwestorów się sprawdzają i cena Y idzie do góry. 6 stycznia 2006 roku cena wzrasta o $10. Wykres 9 i 10 pokazuje sytuację w jakiej Inwestor A i B jest tego dnia. Inwestor B jest już w lepszej sytuacji, a jego ryzyko jest mniejsze, ale to jeszcze nie wszystko. Oglądanie takich symulacji "na sucho" nie odzwierciedla wszystkich możliwości. Bo oto Inwestor B może sprzedać zabezpieczającą opcję put i ustawić "stop" na poziomie 100, Inwestor A natomiast nie może tego zrobić. Jego opcja call to jego pozycja, dlatego musi ją utrzymać lub sprzedać aby zainkasować zysk. Jeśli cena Y wzrośnie jeszcze bardziej, Inwestor B może podwyższać swój potencjalny zysk przez przesuwanie "ruchomego stopu" podczas kiedy Inwestor A wkrótce nie będzie miał takiej możliwości. Jego opcja niedługo wygaśnie, zysk zostanie zrealizowany, a utrzymanie się w trendzie będzie wymagała ponownego otwarcia pozycji, czyli ponownego podjęcia ryzyka.
Wykres 10 Rozkład zysków i strat dla portfela akcji i opcji
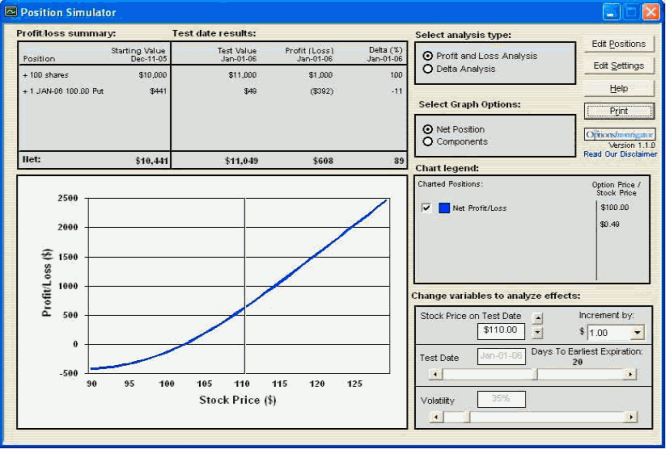
źródło: obliczenia własne przy pomocy programu Option Investigator
Z drugiej strony używanie opcji jako zabezpieczenia pozycji w akcjach może być korzystniejsze niż samo ustawianie stopów. Do podstawowych atutów można zaliczyć:
- możliwość- korzystania z dodatkowych korzyści wynikających z posiadania instrumentu (np. dywidendy, korzyści podatkowe, korzystanie z prawa głosu na WZA),
- niższe koszty wynikające z braku konieczności ponawiania pozycji w wypadku przypadkowego "wyrzucenia" z rynku.
Podane powyżej przykłady to jedne z najbardziej podstawowych doborów techniki operowania opcjami w zależności od potrzeb i warunków na rynku
Dlatego proszę je potraktować jako początkową część "alfabetu" strategii opcji. Więcej przykładów w następnych odcinkach.
Niniejszy materiał, przygotowany przez DM BOŚ S.A. ma charakter wyłącznie informacyjny, prezentowany jest w celach edukacyjnych i nie stanowi porady prawnej oraz nie jest rekomendacją osobistą w ramach świadczenia usługi doradztwa inwestycyjnego zgodnie z przepisami prawa. DM BOŚ S.A. nie udziela gwarancji dokładności, aktualności, oraz kompletności niniejszych informacji. Zaleca się przeprowadzenie we własnym zakresie niezależnego przeglądu informacji z niniejszego materiału.


